Question

If \[ABCD\] is a parallelogram, \[E\] and \[F\] are the midpoint of \[AB\] and \[CD\] .Prove: \[AF\] and \[CE\] trisect the diagonal \[BD.\]

Answer 1

Hint: In this problem, \[ABCD\] is a parallelogram and the midpoint also given in the diagrammatic representation, Parallelogram is defined as a quadrilateral in which both pairs of opposite sides are parallel is called a parallelogram. Here, we use the conversion of the midpoint theorem, the line drawn through the midpoint of one side of a triangle, parallel to another side bisecting the third side.

Complete step-by-step answer:
In the given problem,
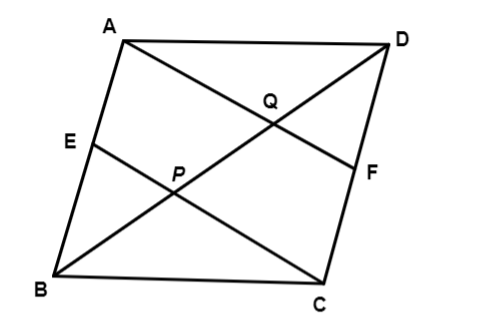
 \[ABCD\] is a parallelogram. \[E\] and \[F\] are the mid-points of sides \[AB\] and \[CD\] respectively.
To show: line segments \[AF\] and \[\;EC\] trisect the diagonal \[BD\] .
Proof,
 \[ABCD\] is a parallelogram
Therefore, \[AB\parallel CD\]
also, \[AE\parallel FC\]
Now,
 \[AB{\text{ }} = {\text{ }}CD\]
(Opposite sides of parallelogram \[ABCD\] )
 \[\dfrac{1}{2}{\text{ }}AB = \dfrac{1}{2}CD\]
 \[AE = FC\]
 Where, \[E\] and \[F\] are midpoints of side \[\;AB\] and \[CD\] .
Since a pair of opposite sides of a quadrilateral \[\;AECF\] is equal and parallel.
so, \[\;AECF\] is a parallelogram
Then, \[AE\parallel EC\] ,
 \[AP\parallel EQ\] and \[FP\parallel CQ\]
Since, opposite sides of a parallelogram are parallel
Now,
In \[\Delta DQC,\]
 \[F\] is midpoint of side \[DC\] and \[FP\parallel CQ\]
(as \[AF\parallel EC\] ).
So, \[P\] is the midpoint of \[DQ\]
 Here, we use converse of midpoint theorem, we get
 \[DP = PQ{\text{ }} \to {\text{(1)}}\]
Similarly,
In \[APB,\]
 \[E\] is the midpoint of side \[AB\] and \[EQ\parallel AP\] (as \[AF\parallel EC\] ).
So, \[Q\] is the midpoint of \[PB\] .
By applying Converse of midpoint theorem, we get
 \[\;PQ = QB \to (2){\text{ }}\]
From equations \[(1)\] and \[(2)\] , we get
 \[DP = PQ = BQ\]
Hence, the line segments \[AF\] and \[EC\] trisect the diagonal \[BD\] .

Note: Here, we have to solve the geometric problem by the diagrammatic representation and here, a parallelogram concept is used and a converse of the midpoint theorem is used. A quadrilateral is a parallelogram if Its opposite sides are equal, its opposite angles are equal, diagonals bisect each other and a pair of opposite sides is equal and parallel.