Question

If each side of the triangle is doubled, then find the ratio of the new triangle thus formed and the given triangle?

Answer 1

Hint: We have to find the ratios so for this first of all we will calculate the area of the triangle by using the heron’s formula and then for the changed triangle again we will find the area of the triangle and then find the ratios between them.

Formula used:
By Heron’s formula
The area of the triangle will be $A = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $
Here,
$A$ , will be the area
$s$ , will be the perimeter
$a,b,c$ , will be the sides of a triangle

Complete step-by-step answer:
Let us assume $a,b,c$ be the different sides of the triangle.

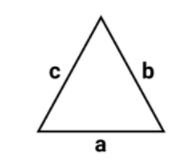
So the perimeter of the triangle will be
$ \Rightarrow 2s = a + b + c$
And for the semi-perimeter, it will be half of it.
So,
$ \Rightarrow s = \dfrac{{\left( {a + b + c} \right)}}{2}$
By Heron’s formula
The area of the triangle will be $A = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $
Now according to the questions, if the sides of the triangle are doubled i.e. it will become $2a,2b,2c$.

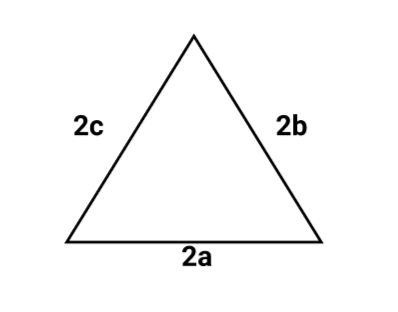
Let us suppose $s'$ be the sides of the semi perimeter of a triangle.
Then its perimeter will be equal to
$ \Rightarrow 2s' = 2a + 2b + 2c$
And on solving, we will get
$ \Rightarrow s' = a + b + c$
And it can also be equal to
$ \Rightarrow s' = 2s$
Now the area of the new triangle will be
$ \Rightarrow A' = \sqrt {s'\left( {s' - 2a} \right)\left( {s' - 2b} \right)\left( {s' - 2c} \right)} $
And on solving the equation and substituting the values $s' = 2s$ we will get
$ \Rightarrow A' = \sqrt {\left( {2s} \right)\left( {2s - 2a} \right)\left( {2s - 2b} \right)\left( {2s - 2c} \right)} $
So while solving the equation, we will get
$ \Rightarrow A' = \sqrt {{2^4}s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $
Taking the power outside we get
$ \Rightarrow A' = 4\sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $
And hence it can also be written as
$ \Rightarrow A' = 4A$
Therefore the ratios of $A':A = 4:1$.
And hence $4:1$ will be the ratio of the area of the new triangle and the old triangle.

Note: So this question can also be solved by using the property of the symmetry and applying the area rule of a triangle. We can get the ratios of the new to the old triangle. We just have to keep in mind the geometry of it if we have to find it with the help of symmetry properties.