Question

If OP = r, d.c’s of \[\overrightarrow{OP}\] are l, m and n then $P=(lr,mr,nr)$.

Answer 1

Hint: To solve this question, we will first write the values of direction cosines in the Cartesian form. After that, we will find the length of line OP which passes through point P ( x, y z ) and origin. After that, we will substitute the value of length OP = r in values of direction cosines and hence obtain the coordinates of P in terms of cosines of line OP.

Complete step-by-step solution
Before we solve this question, let us see what direction cosines are.
In three – dimension geometry, we have three axes which are the x-axis, y-axis, and z-axis. Now, let us assume that line OP passes through the origin in the three – dimensional space. Then, it is obvious that the line will make an angle each with the x-axis, y-axis, and z-axis respectively.
Now, cosines of each of these three angles that the line makes with the x-axis, y-axis, and z-axis respectively are called direction cosines of the line in three-dimensional space. In general, these direction cosines are denoted by using letters l, m, and n.

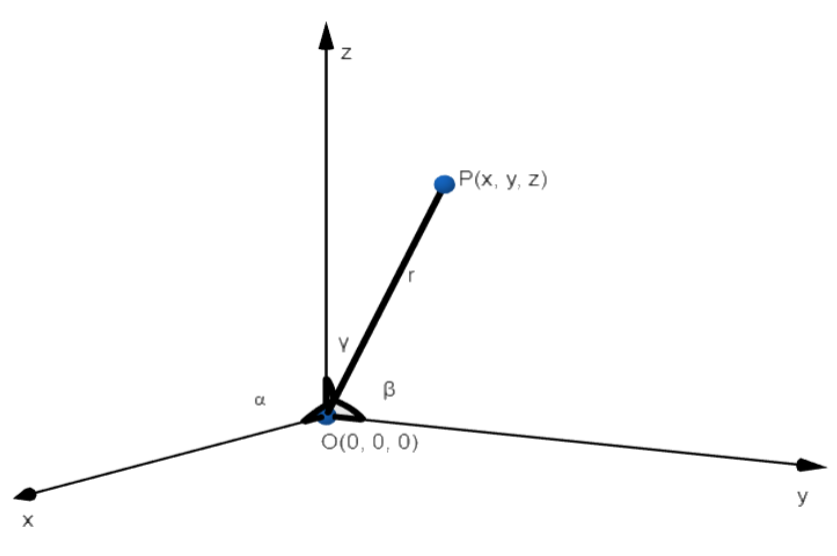
Now, we know that if l, m and n are direction cosines of a line passing through origin to point P(x, y, z), then $l=\dfrac{x}{\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}}$ , $m=\dfrac{y}{\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}}$, $n=\dfrac{z}{\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}}$
Now as OP passes from O( 0, 0, 0 ) and P( x, y, z )
So, using distance formula
$OP=\sqrt{{{(x-0)}^{2}}+{{(y-0)}^{2}}+{{(z-0)}^{2}}}$
On simplifying, we get
$OP=\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}$
As, given that OP = r
So, $r=\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}$
Substituting value of $r=\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}$ in values of direction cosines, we get
$l=\dfrac{x}{r}$ , $m=\dfrac{y}{r}$, $n=\dfrac{z}{r}$
Multiplying, both sides by r, we get
x = lr, y = mr and z = nr
Now, as (x, y, z ) are the coordinates of point P.
So, P ( lr, mr, nr )

Note: Always remember that if line passes through origin and point P ( x, y, z ) then direction cosines of line OP are equals to $l=\dfrac{x}{\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}}$ , $m=\dfrac{y}{\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}}$, $n=\dfrac{z}{\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}}$. Also remember that length of line passing through points L( a, b, c ) and M( x, y, z ) is equals to $LM=\sqrt{{{(x-a)}^{2}}+{{(y-b)}^{2}}+{{(z-c)}^{2}}}$. Try not to make any error while solving the question.