Question

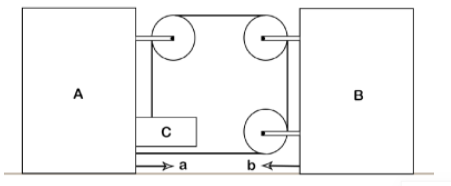
If the blocks A and B are moving towards each other with acceleration a and b as shown in figure. Find the net acceleration of block C.

A. $a\hat{i}-2(a+b)\hat{j}$
B. $-(a+b)\hat{j}$
C. $a\hat{i}-(a+b)\hat{j}$
D. None of these

Answer 1

Hint: Assume the string is ideal. Block C whose acceleration is to be calculated is attached to block A, so x-component of acceleration of block C will be the same as that of block A and its y-component will be in the negative as it will move down towards the negative y-axis.

Complete step by step answer:
We consider the string in question to be an ideal string as it is not given otherwise, if the string can be stretched. As the two blocks A and B move towards each other, the block C will move down towards the negative y-axis. Let us consider the length of strings as
${{L}_{1}},{{L}_{2}},{{L}_{3}}$and ${{L}_{4}}$ as shown in the figure below,

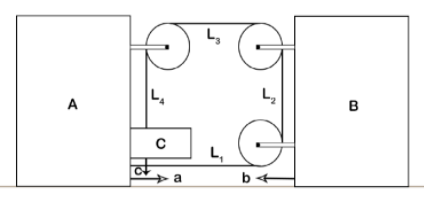
Since it is an ideal string we can write,
${{L}_{1}}+{{L}_{2}}+{{L}_{3}}+{{L}_{4}}=K$ ….(i)
Where, K is a constant.

Now, double differentiating equation(i) with respect to time to get the accelerations,
${{{L}''}_{1}}+{{{L}''}_{2}}+{{{L}''}_{3}}+{{{L}''}_{4}}=0$ ….(ii)

Calculating the values of ${{L}_{1}},{{L}_{2}},{{L}_{3}}$ and ${{L}_{4}}$ as block A and block B accelerates towards each other with acceleration a and b,

${{{L}''}_{1}}=-a-b$ (Since, its length is decreasing as block A and block b come closer to each other.)
${{{L}''}_{2}}=0$ (Since, its length is neither increasing nor decreasing.)
${{{L}''}_{3}}=-a-b$ (Since, its length is also decreasing as block A and block b come closer to each other.)
${{{L}''}_{4}}=c$ (It is the same as acceleration of block C.)

Putting the above values in equation(ii) and solving for c, we get y-component of the acceleration of block C as,

$c=-2(a+b)\hat{j}$ (The negative sign implies the motion is towards negative y-direction.)
The x-component of acceleration of block C is the same as block A as they are attached to each other and move together with acceleration a towards positive x-direction.
Hence, the net acceleration of block C is,
$\vec{c}=a\hat{i}-2(a+b)\hat{j}$

Therefore, the correct answer is option A.

Note:
It is important to affirm if the string in question is an ideal string or one that can be stretched, if nothing about the string is mentioned in the question then students should assume it as an ideal string and thus proceed further to solve the question accordingly.