Question

If the diagonals of a quadrilateral divide each other proportionally, then prove that the quadrilateral is a trapezium.

Answer 1

Hint: Show that the two vertically opposite triangles formed by the diagonals are similar. Then show that alternate angles are equal and prove that this happens when the two lines are parallel.

Complete step-by-step answer:
In Euclidean geometry, a quadrilateral with at least one pair of parallel sides is referred to as a trapezium. A trapezium is 2-D shape. For a quadrilateral to be referred to as a trapezium, it must have only one side parallel and the other two sides should be non-parallel. The parallel sides of a trapezium are called bases and non parallel sides are called legs. If a trapezium has both pairs of its parallel then it is called a parallelogram. Therefore, we can say that every parallelogram is also a trapezium. There are different types of trapezium which are isosceles trapezium, scalene trapezium and a right trapezium. An isosceles trapezium has its non parallel sides equal. A scalene trapezium has all the sides and angles of different measures. A right trapezium has minimum two right angles.

Now, let us come to the question. it is given that the diagonals of the provided quadrilateral divide each other proportionally. Therefore,

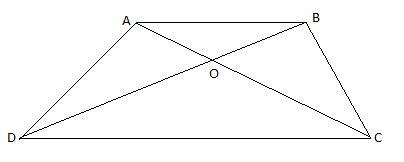
$\begin{align}
  & \dfrac{AO}{OC}=\dfrac{BO}{OD} \\
 & \\
\end{align}$
\[\therefore \dfrac{AO}{BO}=\dfrac{OC}{OD}...................(i)\]
Also, angle AOB and angle COD are equal because they are vertically opposite angles. Hence, $\angle AOB=\angle COD..............(ii)$

From relation (i) and (ii) we can conclude that triangle AOB and COD are similar by SAS similarity criteria.

Hence, $\angle OAB=\angle OCD$. But these are the pair of alternate angles formed when two parallel lines are intersected by a transversal. Hence, sides AB and CD are parallel. Therefore, the given quadrilateral is a trapezium.

Note: In the above solution we have used SAS similarity criteria. This is used when the ratio of two sides and the angle between those two sides of a triangle are equal to the ratio of two sides and the angle between those two sides of another triangle.