Question

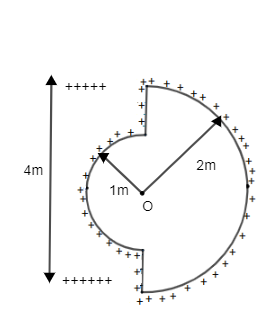
If the $\lambda =1\mu C/m,$ then electric field intensity at O is:

$\begin{align}
  & A.\text{ }9N/C \\
 & B.\text{ }900N/C \\
 & C.\text{ }9000N/C \\
 & D.\text{ }9\times {{10}^{9}}N/C \\
\end{align}$

Answer 1

Hint: In order to find the solution of this equation we will use the formula related linear charge density ($\lambda $) and the electric field density and that is $E=\dfrac{2k\lambda }{r}$ by using this equation we will get electric field intensity at point o.

Formula used:
$E=\dfrac{2k\lambda }{r}$
E = electric field intensity
$\lambda $= linear charge density
r = distance r from the line

Complete step-by-step answer:
Now it is given that in the question that the value of the linear charge density is
$\lambda =1\mu C/m$
$\to $ So if we convert from $\mu C/m$ to C/m we have to multiply by ${{10}^{-6}}$ now the value of the linear charge density is
$\lambda =1\times {{10}^{-6}}C/m$

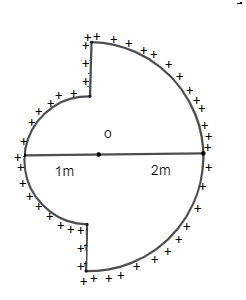
$\to $Now the electric field intensity at the distance from 1m is given by
${{E}_{1}}=\dfrac{2k\lambda }{r}$
Here the value of k is given by $9\times {{10}^{9}}$
$\begin{align}
  & {{E}_{1}}=\underset{1}{\mathop{2\times 9\times {{10}^{9}}\times 1\times {{10}^{-6}}}}\, \\
 & {{E}_{1}}=18\times {{10}^{3}}N/C......\left( 1 \right) \\
\end{align}$
$\to $Now the electric field intensity at distance from 2m is given by
$\begin{align}
  & {{E}_{1}}=\underset{2}{\mathop{2\times 9\times {{10}^{9}}\times 1\times {{10}^{-6}}}}\, \\
 & {{E}_{1}}=9\times {{10}^{3}}N/C......\left( 2 \right) \\
\end{align}$
$\to $Now the total electric field intensity at point o is given by
$E={{E}_{1}}-{{E}_{2}}......\left( 3 \right)$
$\to $Now substitute the value of the equation (1) and (2) in equation (3) to get electric field intensity at point o.
$\begin{align}
  & E=18\times {{10}^{3}}-9\times {{10}^{3}} \\
 & =\left( 18-9 \right)\times {{10}^{3}} \\
 & =9\times {{10}^{3}}N/C \\
 & E=9000N/C \\
\end{align}$
Hence the correct option is (C) 9000N/C

So, the correct answer is “Option C”.

Additional Information: In this question value of the k is given by $\dfrac{1}{4\pi {{\varepsilon }_{0}}}$ because the initial equation of the electric field intensity is
$E=\dfrac{\lambda }{2\pi {{\varepsilon }_{0}}r}$
Then we can substitute$\dfrac{1}{2\pi {{\varepsilon }_{0}}}$ by
$\begin{align}
  & 2k=2\left( \dfrac{1}{4\pi {{\varepsilon }_{0}}} \right) \\
 & 2k=\dfrac{1}{2\pi {{\varepsilon }_{0}}} \\
\end{align}$
Hence our equation will become
$E=\dfrac{2k\lambda }{r}$
Hence the correct option is (C).

Note: As shown in the figure that when the positive (+ve) charge is considered at a point o then from the both the sides the linear charge density will be opposite from the both the sides at the point o.