Question

If the length of a common internal tangent to two circles is 7 and that of a common external tangent is 11, then the product of the radii of two circles is
(a)36
(b)9
(c)18
(d)4

Answer 1

Hint: Here, we have to draw two figures, one figure with common external tangent and the other figure with common internal tangent. Here, there will be a larger circle and a smaller take the radius of the larger circle as a and the smaller circle as b and d be the distance between the two centres. Now, from the two figures we will get two right angled triangles and by applying Pythagoras theorem we will get two equations. By solving the equations we will get the product of radii of two circles.

Complete step-by-step answer:

Here, we are given that the length of a common internal tangent to two circles is 7 and that of a common external tangent is 11.

Now, we have to find the product of radii of two circles.

First let us draw the figure consisting of a common external tangent.

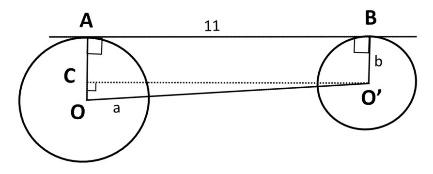
Here, let us take d as the distance between the centres of the two circles. Let a be the radius of the larger circle, the circle with centre O and b be the radius of the smaller circle, the circle with centre O’.

Next, we can draw a line from O’ which is parallel To AB and meets OA at C. hence we can say that O’C is perpendicular to OA and O’C is also the length of the common external tangents A and B which is 11

Now, consider the right angled triangle $\Delta OCO'$. Here, we can apply the Pythagoras theorem, which says that the square of the hypotenuse side is the sum of the squares of its base and height. Hence, we have:

$OO{{'}^{2}}=O'{{C}^{2}}+O{{C}^{2}}$ ….. (1)

We know that the distance between two centres is OO’ and it is d.

O’C is the length of the common external tangent. Therefore, we can write:

$O'C=11$

$OC=OA-AC$

OA is the radius of the circle with centre O. Here, we have taken radius as a, i.e.

\[OA=a\]

From the figure we can also say that:

$AC=O'B=b$

Now, by substituting these values we get:

$OC=a-b$

 Now, by substituting the values of OC, O’C and OO’ our equation (1) becomes:

$\begin{align}

  & {{d}^{2}}={{11}^{2}}+{{(a-b)}^{2}} \\

 & {{d}^{2}}=121+{{(a-b)}^{2}} \\

\end{align}$

Now by expanding ${{(a-b)}^{2}}$ we get:

${{(a-b)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}$

Therefore, by substituting the above expansion in equation (2), we obtain:

${{d}^{2}}=121+{{a}^{2}}-2ab+{{b}^{2}}$ ….. (3)

Next, we also have that the length of the internal tangent of two circles is 7. So we can draw another figure consisting of a common internal tangent.

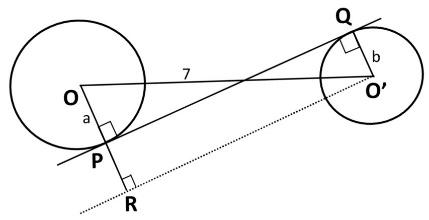
From the figure, we can say that there are two circles, a larger circle with centre O and a smaller circle with centre O’. Let a be the radius of the larger circle and b be the radius of the smaller circle.

Here, P and Q are the points where the tangent touches the circle and the length of PQ is given as 7. O’O is the distance between the two centres.

Now, by joining O’R we get O’R perpendicular to OR.

Next, consider the right angled triangle $\Delta ORO'$. Now, by Pythagoras theorem we have:

 $OO{{'}^{2}}=O'{{R}^{2}}+O{{R}^{2}}$ ….. (4)

We have $OO'=d$

$\begin{align}

  & O'R=PQ=7 \\

 & OR=OP+PR \\

 & OR=a+b \\

\end{align}$

In the next step, we have to substitute all these values in equation (3). So, our equation becomes:

${{d}^{2}}={{7}^{2}}+{{(a+b)}^{2}}$

Now, by expanding ${{(a+b)}^{2}}$ we get:

${{(a+b)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$

Hence, we will obtain:

${{d}^{2}}=49+{{a}^{2}}+2ab+{{b}^{2}}$ ….. (5)

Now, by equating equation (3) and equation (5) we obtain:

$121+{{a}^{2}}-2ab+{{b}^{2}}=49+{{a}^{2}}+2ab+{{b}^{2}}$

Next, by taking constants to one side and variables to the other side we get:

${{a}^{2}}-2ab+{{b}^{2}}-{{a}^{2}}-2ab-{{b}^{2}}=49-121$

Next, by adding and subtracting the similar terms we obtain:

$-4ab=-72$

Now, by cross multiplication we get:

$ab=\dfrac{-72}{-4}$

By cancellation we get:

$ab=18$

Therefore, we can say that the product of radii of two circles is 18.

Hence, the correct answer for this question is option (c).


Note: Here, we have two tangents, internal tangent and external tangent. A common internal tangent intersects the line segment connecting the centres of the two circles whereas the common external tangent does not intersect.