
If the volume of the cube is
(a) 12 cm
(b) 14 cm
(c) 16 cm
(d) 24 cm
Answer
503.7k+ views
Hint: To solve the given question, we will first find out what a cube is and what the formula to calculate the volume of the cube is. After doing this, we will assume that the side length of a cube is ‘s’ cm. Then we will apply the formula for the volume of the cube. On doing this, we will get the equation,
Complete step-by-step answer:
Before we start to solve the given question, we must know what a cube is. A cube is a three – dimensional object bounded by six square faces or sides with three meetings at each vertex. Now, we will assume that the length of each side of the cube is ‘s’ cm.
Now, we know that the volume of the cube is given by the formula shown below.
In our case,
On taking the cube root on both the sides of the above equation, we will get the following equation
Now, we will find the cube root of 1728 using the prime factorization method. In this method, we will try to write 1728 as the product of the prime numbers. Thus, we have,
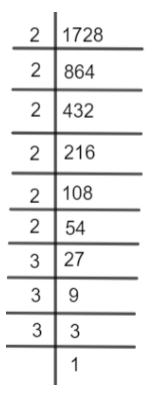
Thus, we can say that,
Now, we will put the value of 1728 from (ii) to (i). Thus, we will get,
Hence, option (a) is the right answer.
Note: The prime factorization method with the help of which we have found out the cube root of 1728 is not valid every time. We can use this method only when the number of which we have to find the cube root is the perfect cube of an integer. Do not make the silly mistake of finding the square root instead of the cube root of the volume and reporting it as the side of the cube.
Complete step-by-step answer:
Before we start to solve the given question, we must know what a cube is. A cube is a three – dimensional object bounded by six square faces or sides with three meetings at each vertex. Now, we will assume that the length of each side of the cube is ‘s’ cm.

Now, we know that the volume of the cube is given by the formula shown below.
In our case,
On taking the cube root on both the sides of the above equation, we will get the following equation
Now, we will find the cube root of 1728 using the prime factorization method. In this method, we will try to write 1728 as the product of the prime numbers. Thus, we have,

Thus, we can say that,
Now, we will put the value of 1728 from (ii) to (i). Thus, we will get,
Hence, option (a) is the right answer.
Note: The prime factorization method with the help of which we have found out the cube root of 1728 is not valid every time. We can use this method only when the number of which we have to find the cube root is the perfect cube of an integer. Do not make the silly mistake of finding the square root instead of the cube root of the volume and reporting it as the side of the cube.
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What are the public facilities provided by the government? Also explain each facility

Difference between mass and weight class 10 physics CBSE

SI unit of electrical energy is A Joule B Kilowatt class 10 physics CBSE




