Question

If two sides of a triangle are unequal, the angle opposite to the longer side is larger (or greater). You may prove this theorem by taking a point P on BC such that CA = CP.

Answer 1

Hint: First write the theorem clearly and understand the term present in the theorem. Take a point opposite to the general angle, such that the distance of a point from the vertices is the same as the distance between the vertices. Use the theorems you know on the sides and prove the required theorem.

Complete step-by-step answer:
Given theorem in the question can be written in the form of:
If two sides of a triangle are unequal, the angle opposite to the longer side is larger.
Let us assume a triangle ABC such that the sides are as AB > AC.

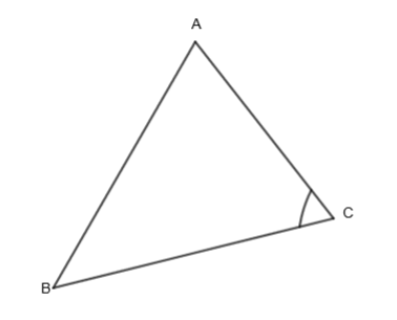
By theorem, we need to prove that angle C > angle B.
Now, take a point P on line AB such that AP = AC. Join the two points C and P to set CP. Let us assume angle APC is \[{{x}^{o}}\] and angle BCP is \[{{y}^{o}}.\]

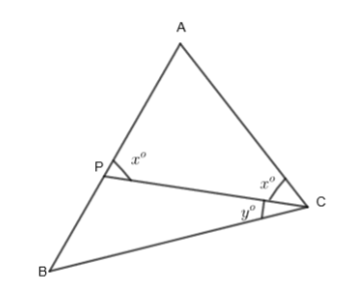
We know that AP = AC. If two sides are equal in a triangle, then the angles opposite to the sides are equal. Applying this condition to the triangle APC, we get the angle APC and angle ACP, all equal. As angle APC is \[{{x}^{o}},\] we get the angle ACP also \[{{x}^{o}}.\] Mathematically, we write these steps as follows:
\[\angle ACP=\angle APC\]
\[\angle ACP={{x}^{o}}\]
On line AB, we can say that it is a straight line which is equal to \[{{180}^{o}}.\] So, we get,
\[\angle APC+\angle CPB={{180}^{o}}\]
By substituting the value of angle APC, we get the equation as,
\[x+\angle CPB={{180}^{o}}\]

By subtracting x on both the sides of the equation, we get it as,
\[\angle CPB={{180}^{o}}-x\]
We know the theorem that sum of all the angles in a triangle is \[{{180}^{o}}.\] By applying this to the triangle CPB, we get it as,
\[\angle CBP+\angle BPC+\angle PCB={{180}^{o}}\]
By substituting the value of BPC from the above equation, we get,
\[\angle CBP+{{180}^{o}}-x+\angle PCB={{180}^{o}}\]
By substituting the value of PCB as per our assumption, we get,
\[\angle CBP+{{180}^{o}}-x+y={{180}^{o}}\]
By canceling out the common terms, we can write it as,
\[\angle CBP-x+y=0\]
By adding x and subtracting y on both the sides, we get,
\[\angle CBP=x-y\]
From the diagram, we can say that,
\[\angle CBP=\angle CBA\]
\[\angle CBA=x-y.....\left( i \right)\]
From the diagram, we can say that,
\[\angle BCA=\angle BCP+\angle PCA\]
By substituting the values, we get it in the form of
\[\angle BCA=x+y....\left( ii \right)\]
From (i) and (ii), we can say the inequality in the form of
\[\angle BCA>\angle CBA\]
\[\Rightarrow \angle C>\angle B\]
Hence, we have proved that the angle opposite to the greater side is larger.

Note: Be careful while marking the angles in the diagram. As when you miss any angle, you may not get the idea to proceed. The idea of making the angles as sum, the difference of angles is very important. This is derived from a small idea that the sum is greater than the difference if the numbers are positive. Here, the angles are positive.