Question

Why is the impedance LCR circuit capacitive at a frequency lower than resonant frequency?

Answer 1

Hint:In order to answer this question, first we will understand the concept of resonant frequency. Then, we will consider the different cases in which the value of frequency is lower, higher or equal to the resonant frequency. This way we will get the answer.

Complete step by step solution:
LCR circuit is an electrical circuit which consists of three elements. These three elements are Inductor, Resistor and Capacitor. These elements can either be connected in series or in parallel. In this particular question these three elements are connected in series. So, the diagram for a series LCR circuit is:

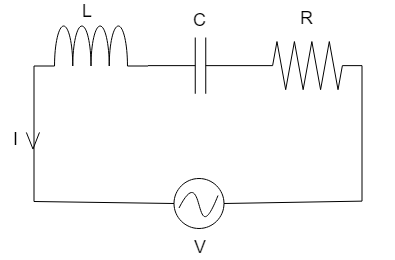
Resonance is the phenomenon in the circuit when the output of that electric circuit is maximum at one particular frequency. In an LCR circuit, this frequency is determined by the values of inductance, conductance, and resistance.
$Z = \sqrt {{R^2} + {{\left( {{X_L} - {X_C}} \right)}^2}} ......(1)$
Where,
$Z$ is the impedance
$R$ is the resistance
${X_L}$ is the inductive reactance
${X_C}$ is the capacitive reactance
The value of inductive reactance ${X_L}$ is given by the expression,
${X_L} = \omega L....(2)$
We also know that $\omega = 2\pi f$
So, we can write equation (2) as,
${X_L} = 2\pi fL.....(3)$
Similarly, the value of inductive reactance ${X_C}$ is given by the expression,
${X_C} = \dfrac{1}{{\omega C}}....(4)$
We also know that $\omega = 2\pi f$
So, we can write equation (4) as,
${X_C} = \dfrac{1}{{2\pi fC}}.....(5)$
At resonance, we know that the value of the inductive reactance and capacitive reactance becomes equal, so the value of impedance is minimum and hence, the current is maximum.
So, the condition for resonance is,
${X_L} = {X_C}$
On putting the value of ${X_L}$ and ${X_C}$ from equation (3) and equation (5), we get,
$2\pi fL = \dfrac{1}{{2\pi fC}}$
${f^2} = \dfrac{1}{{4{\pi ^2}LC}}$
On taking square root on both the sides, we get,
$f = \dfrac{1}{{2\pi \sqrt {LC} }}$
This is the expression for the resonant frequency.
But if the frequency is lower than the resonant frequency, then from equation (3) we can say that the value of the inductive reactance ${X_L}$ also decreases as there is a direct relation between them. Similarly, when the value of the frequency is lower than the resonant frequency, then from equation (5) we can say that the value of capacitive reactance increases as there is an inverse relation between them. So, we can clearly see that when the frequency is lower than the resonant frequency, then the impedance LCR circuit is capacitive in nature.

Note:
We have understood that when the value of frequency is lower than the value of resonant frequency, then the impedance LCR circuit is capacitive in nature. Similarly, when the value of frequency is higher than the value of resonant frequency, then the impedance LCR circuit is inductive in nature.