Question

In a cathode ray tube if V is the potential difference between the cathode and anode, the speed of electrons, when they reach the anode is proportional to
(Assume initial velocity = 0)
A. $V$
B. $\dfrac{1}{V} $
C. $\sqrt V $
D. $\dfrac{{{v^2}}}{{2em}} $

Answer 1

Hint: This problem can be solved by the concept of the principle of conservation of energy. Here, we have to establish the difference between the kinetic energy of the electron and the electrical potential energy to solve the question.

Complete step by step answer:
In a cathode ray tube, the electron, that is emitted from the negatively charged cathode, is accelerated across the tube from the cathode to the positively charged anode.

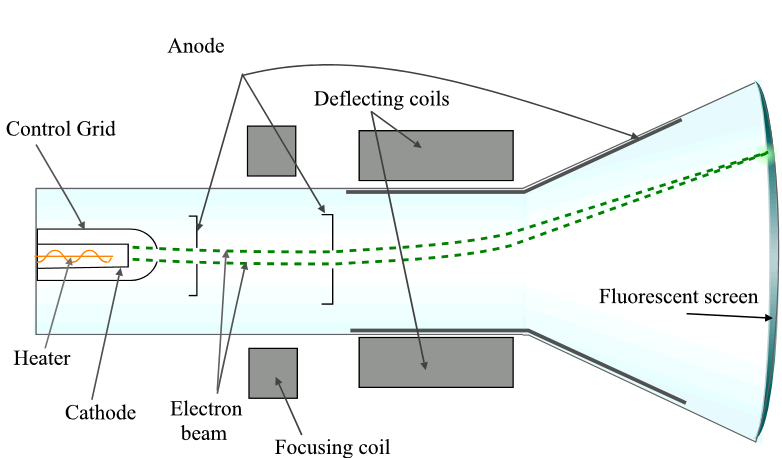
Since the electron is in motion, it has kinetic energy associated with it:
The kinetic energy of the electron, $KE = \dfrac{1}{2}m{v^2}$
where $m$ is the mass of the electron and $v$ is the velocity of the electron.
The reason for driving the electron from cathode to anode is the electrostatic potential difference. Thus, there is a potential difference acting on the electron which is moving from cathode to anode.
The electric potential energy acting on the electron is $E = eV$
where,
$V$= potential difference between the cathode and anode.
$e$= charge of one electron
As per the law of conservation of energy, the kinetic energy of the electron to travel from cathode to anode is provided by the electric potential energy.
This means that $KE = E$
Substituting the values,
$\dfrac{1}{2}m{v^2} = eV$
Rearranging the equation, we get
$
  \dfrac{1}{2}m{v^2} = eV \\
 \Rightarrow {v^2} = \dfrac{{eV \times 2}}{m} \\
 $
Here, the mass of the electron and the charge on the electron are constant values:
$
{v^2} = \left( {\dfrac{{2e}}{m}} \right)V \\
\Rightarrow {v^2} \propto V \\
\Rightarrow v \propto \sqrt V \\
 $
From this equation, it is proven that the velocity of the electron is proportional to the square root of the potential difference between the cathode and anode $\left( {\sqrt V } \right)$. So, option (C) is correct.

Note:
While solving the actual problems with values, you must be careful about the units of energy. The units of energy for huge objects in motion are joules (J) and the units of energy for tiny objects in motion such as an electron is in the unit electron-volt (eV). One must exercise caution while dealing with the energy units in the question. The conversion is as follows:
$1eV = 1.602 \times {10^{ - 19}}J$