Question

In a convex nonagon all the diagonals are drawn. These diagonals intersect each other at $p$ points inside the nonagon, $q$ points on the nonagon and $r$ points outside the nonagon. Find the maximum possible value of $p$ . \[\]

Answer 1

Hint: Draw possible figures of the convex nonagon and use the concept of convexity to find that find out that diagonals can only intersect inside. Find how many vertices are required for one point of intersection of diagonals and then you can use a combination formula to get the result. \[\]

Complete step by step answer:
A nonagon is a polygon with 9 equal sides and 9 vertices. It is given in the question that the nonagon is convex; that means if we take any two points inside the nonagon and join the line segment all the points of the line segment will lie inside the nonagon. We also know that in a convex nonagon no angles are greater than straight angles. \[\]
The given question states that the diagonals intersect each other at $p$ points inside the nonagon, $q$ points on the nonagon and $r$ points outside the nonagon but asks only the maximum value of $p$. \[\]
Let us consider the possible diagonals inside the nonagon. Let us take alternating vertices (leaving one vertex and joining the next ) and join them to find a point of intersection. We show this in the following figure \[\]
 

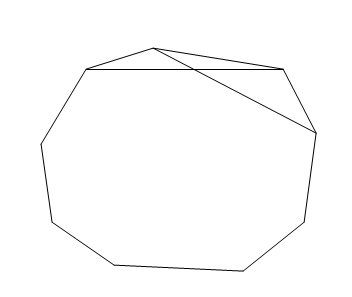
Let us join a pair of vertices who have two vertices between them. We take another such pair of vertices and join them to find a point of intersection. We show this in the following figure. \[\]

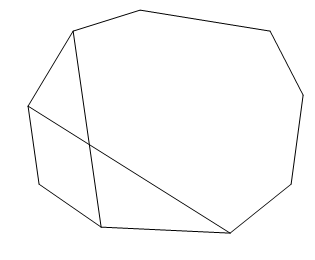
 We can also join a pair of alternating vertices and a pair of vertices with two vertices in between them. We show this by the following figure. \[\]
 

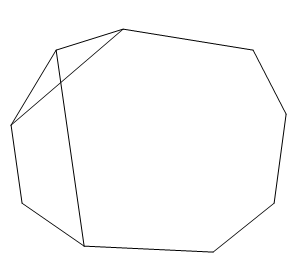
We draw the figure to illustrate that there are no points of intersection of diagonals outside the nonagon. We see that the nonagon is convex which means the diagonal can only intersect in the interior of the nonagon. \[\]

We also observe from the figure that we need at least 4 vertices to find one point of intersection. So we can choose any 4 out 9 vertices and can find a point of intersection. So we use the combination formula $^{n}{{C}_{r}}=\dfrac{n!}{r!\left( n-r \right)!}$ for selecting any 4 vertices out 9 and get
\[^{9}{{C}_{4}}=\dfrac{9!}{4!5!}=\dfrac{9\times 8\times 7\times 6\times 5!}{1\times 2\times 3\times 4\times 5!}=126\]

So the maximum value of $p$ is 126.

Note: The important word in this problem is convex which means we do not have to care about points of intersection outside the nonagon which is the case of concave nonagon. The extra information about points of intersection on and outside nonagon is there to distract only.