Question

In a line of sight radio communication, a distance of about 50 km is kept between the transmitting and receiving antennas, If the height of the receiving antenna is 70 m, then the minimum height of the transmitting antenna should be:
(Radius of earth $=6.4\times {{10}^{6}}m$)
A). 40 m
B). 51 m
C). 32 m
D). 20 m

Answer 1

Hint: learn about the transmission of radio waves. Study how space waves propagate. understand what is line of sight propagation. Obtain the equation that gives the range of space wave propagation and put the given values to find the required answer.

Formula used:
$\text{Range }=\sqrt{2R{{h}_{T}}}+\sqrt{2R{{h}_{R}}}$

Complete step by step answer:
A way of propagating radio waves is through space waves. A space wave propagates from the transmitting antenna to the receiving antenna in a straight line of sight. Because of straight line of sight propagation at a point this wave is blocked because of the curvature of earth's surface. So, we have a definite range for this type of wave.

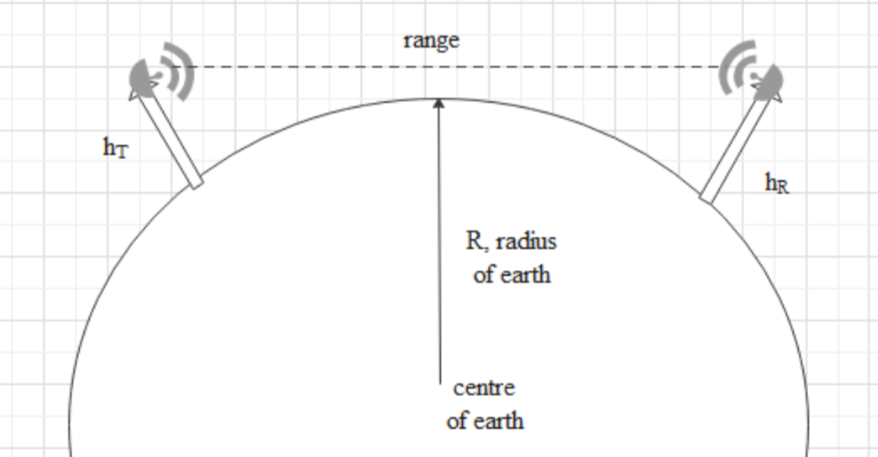
We are given that the height of the receiving antenna is, ${{h}_{R}}=70m$
The range of the radio communication is given s, $50km=5\times {{10}^{4}}m$
Radius of earth is given as, $R=6.4\times {{10}^{6}}m$
We can express the relation between the range of the radio communication and the height of the transmission antenna and the receiving antenna as,
$\text{Range }=\sqrt{2R{{h}_{T}}}+\sqrt{2R{{h}_{R}}}$
Where, ${{h}_{T}}$ is the height of the transmission antenna.
Putting the values of the given quantities, we get that,
$\begin{align}
  & 5\times {{10}^{4}}=\sqrt{2\times 6.4\times {{10}^{6}}\times {{h}_{t}}}+\sqrt{2\times 6.4\times {{10}^{6}}\times 70} \\
 & 5\times {{10}^{4}}=3.57\times {{10}^{3}}\times \sqrt{{{h}_{t}}}+3\times {{10}^{4}} \\
 & 3.57\times {{10}^{3}}\times \sqrt{{{h}_{t}}}=\left( 5-3 \right)\times {{10}^{4}} \\
 & \sqrt{{{h}_{t}}}=\dfrac{2\times {{10}^{4}}}{3.57\times {{10}^{3}}} \\
 & \sqrt{{{h}_{t}}}=5.61 \\
 & {{h}_{t}}=31.4 \\
 & {{h}_{t}}\approx 32m \\
\end{align}$
So, the height of the transmitting antenna will be, 32m.
The correct option is (C).

Note: We have other types of radio wave transmissions also. In ground wave transmission we should have an antenna with size comparable to the wavelength. In sky wave propagation we use the ionosphere to reflect the radio waves.
In the space wave for one antenna with height h, the distance to the horizon is given by $\sqrt{2Rh}$. For the two antennas range is given by the addition of these two distances.