Question

In a liquid medium of dielectric constant \[K\] and of specific gravity \[2\] , two identically charged spheres are suspended from a fixed point by threads of equal lengths. The angle between them is \[90\,^\circ \]. In another medium of unknown dielectric constant \[{K^1}\] , and specific gravity \[4\] , the angle between them becomes \[120\,^\circ \] if the density of the material of spheres is \[8\,{\text{g}}\,{\text{c}}{{\text{m}}^{ - 3}}\] . Then \[{K^1}\] is:
A. \[\dfrac{K}{2}\]
B. \[\dfrac{{\sqrt 3 }}{K}\]
C. \[\dfrac{{\sqrt 3 }}{2}K\]
D. \[\dfrac{K}{{\sqrt 3 }}\]

Answer 1

Hint: First of all, we will draw the diagram, showing all the components of forces. We will equate the horizontal and the vertical forces separately and combine them for the two different cases given in the question. By substituting the required values in the equation followed by manipulation, we will find the desired result. The angle that we will take is the angle of the string of the spheres about the mean position.

Complete step by step solution:
In the given problem, we are supplied the following data:
There is a liquid medium whose dielectric constant is \[K\] and of specific gravity is \[2\] .
There are two spheres which are suspended from a fixed point by threads of equal lengths.In this case the angle between the two charged spheres is \[90\,^\circ \].Again, there is another medium whose dielectric constant is \[{K^1}\] and the specific gravity is \[4\] .In this case, the angle between the two spheres is \[120\,^\circ \] .The density of the material of the spheres is \[8\,{\text{g}}\,{\text{c}}{{\text{m}}^{ - 3}}\] .We are asked to find the value of the unknown dielectric constant.

To begin with, let us understand the situation first about the alignment of the two spheres in both the cases.In the first case, the angle separating the two spheres is \[90\,^\circ \] . So, the angle of the thread joining each sphere from the normal position will definitely be \[45\,^\circ \] i.e. \[\dfrac{{90\,^\circ }}{2}\] .In the first case, the angle separating the two spheres is \[120\,^\circ \] . So, the angle of the thread joining each sphere from the normal position will definitely be \[60\,^\circ \] i.e. \[\dfrac{{120\,^\circ }}{2}\] .For better understanding we will draw a diagram showing all the components of the forces. The diagram is given below:

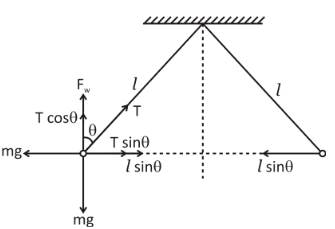
The distance between the two spheres will be then:
$l\sin \theta + l\sin \theta \\
= 2l\sin \theta \\$
From the diagram, we can say that the horizontal force is equal to the \[T\sin \theta \] component of the tension force.
Let the volume of the sphere is \[V\] .
The vertical force is equivalent to \[{F_{\text{w}}} = {\rho _1}Vg\] .
The weight of the sphere is equivalent to \[mg = \rho Vg\] .

So, for the first case, we can take the force as:
\[F = T\sin \theta \]
So, we now expand the above equation as follows:
$F = T\sin \theta \\
\Rightarrow \dfrac{1}{{4\pi {\varepsilon _0}K}} \times \dfrac{{{q^2}}}{{{{\left( {2l\sin \theta } \right)}^2}}} = T\sin \theta \\$
\[ \Rightarrow T\sin \theta = \dfrac{{{q^2}}}{{16\pi {\varepsilon _0}K{l^2}{{\sin }^2}\theta }}\] …… (1)
Again, we can write by balancing the vertical force:
\[{F_{\text{w}}} + T\cos \theta = mg\]
\[ \Rightarrow T\cos \theta = mg - {F_{\text{w}}}\] …… (2)
Now, we divide the equations (1) and (2) and we get:
$\dfrac{{T\sin \theta }}{{T\cos \theta }} = \dfrac{{\dfrac{{{q^2}}}{{16\pi {\varepsilon _0}K{l^2}{{\sin }^2}\theta }}}}{{mg - {F_{\text{w}}}}} \\
\Rightarrow T\tan \theta = \dfrac{{\dfrac{{{q^2}}}{{16\pi {\varepsilon _0}K{l^2}{{\sin }^2}\theta }}}}{{\rho Vg - {\rho _1}Vg}} \\$
\[ \Rightarrow T\tan \theta = \dfrac{{{q^2}}}{{16\pi {\varepsilon _0}K{l^2}{{\sin }^2}\theta }} \times \dfrac{1}{{Vg\left( {\rho - {\rho _1}} \right)}}\] …… (3)
Putting the values for the first case the equation (3) becomes:
\[T\tan 45^\circ = \dfrac{{{q^2}}}{{16\pi {\varepsilon _0}K{l^2}{{\sin }^2}45^\circ }} \times \dfrac{1}{{Vg\left( {8 - 2} \right)}}\]
\[ \Rightarrow T\tan 45^\circ = \dfrac{{{q^2}}}{{16\pi {\varepsilon _0}K{l^2}{{\sin }^2}45^\circ }} \times \dfrac{1}{{6Vg}}\] …… (4)
Putting the values for the second case the equation (3) becomes:
\[T\tan 60^\circ = \dfrac{{{q^2}}}{{16\pi {\varepsilon _0}{K^1}{l^2}{{\sin }^2}60^\circ }} \times \dfrac{1}{{Vg\left( {8 - 4} \right)}}\]
\[ \Rightarrow T\tan 60^\circ = \dfrac{{{q^2}}}{{16\pi {\varepsilon _0}K{l^2}{{\sin }^2}60^\circ }} \times \dfrac{1}{{4Vg}}\] …… (5)

Now, we divide the equations (4) and (5) and we get:
$\dfrac{{T\tan 45^\circ }}{{T\tan 60^\circ }} = \dfrac{{\dfrac{{{q^2}}}{{16\pi {\varepsilon _0}K{l^2}{{\sin }^2}45^\circ }} \times \dfrac{1}{{6Vg}}}}{{\dfrac{{{q^2}}}{{16\pi {\varepsilon _0}{K^1}{l^2}{{\sin }^2}60^\circ }} \times \dfrac{1}{{4Vg}}}} \\
\Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{{K^1}{{\sin }^2}60^\circ }}{{K{{\sin }^2}45^\circ }} \times \dfrac{4}{6} \\
\Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{{K^1} \times \dfrac{3}{4}}}{{K \times \dfrac{1}{2}}} \times \dfrac{2}{3} \\
\therefore {K^1} = \dfrac{K}{{\sqrt 3 }}$
Hence, the value of the unknown dielectric constant is \[\dfrac{K}{{\sqrt 3 }}\] .

The correct option is D.

Note:While solving this problem, remember that it is very important to resolve all the forces which are actually acting on the spheres. In failure to do so or if we miss even one component of force, then it will produce irrelevant results. Many students tend to make a common mistake by taking the angles as given in the questions itself. Rather we should take their halves about their mean position.