Question

In a quadrilateral ABCD, the angles A, B, C and D are in the ratio 1 : 2 : 3 : 4. Find the measure of each angle of the quadrilateral.

Answer 1

Hint – In this particular question use the concept that in a quadrilateral the sum of all the angles is equal to 360 degrees, and assume any variable for the angle A, and remaining angles are the multiplication of the variable and the respective ratio number so use these concepts to reach he solution of the question.

Complete step by step solution:

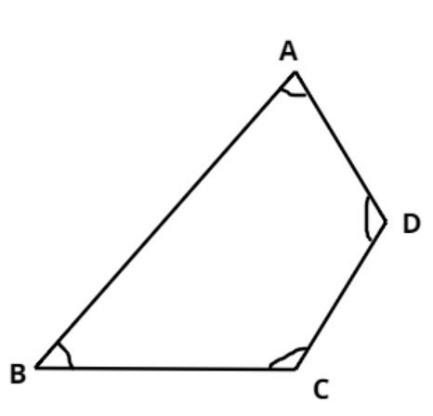
Given data:
Angles of quadrilateral A, B, C and D are in the ratio 1 : 2 : 3 : 4.
Therefore,
$\angle A:\angle B:\angle C:\angle D = 1:2:3:4$
Now let, angle A = x.
Therefore, angle B = 2x, angle C = 3x and angle D = 4x.
Now as we all know that in a quadrilateral the sum of all the angles is equal to 360 degrees.
Therefore, sum of all the angles in a quadrilateral = ${360^\circ}$
Therefore, $\angle A + \angle B + \angle C + \angle D = {360^\circ}$
Now substitute the values we have,
Therefore, x + 2x + 3x + 4x = ${360^\circ}$
Now simplify the above equation we have,
Therefore, 10x = ${360^\circ}$
Now divide by 10 throughout we have,
Therefore, x = (${360^\circ}$/10) = ${36^\circ}$
So the value of angle A = ${36^\circ}$
Value of angle B = 2(${36^\circ}$) = ${72^\circ}$
Value of angle C = 3(${36^\circ}$) = ${108^\circ}$
Value of angle D =4(${36^\circ}$) = ${144^\circ}$
So these are the values of the angles of the quadrilateral.
So this is the required answer.

Note –Whenever we face such types of questions the key concept we have to remember is that always recall the conditions on angle in a quadrilateral such as the sum of the opposite angle in a quadrilateral is 180 degrees and the second condition is stated above these conditions are really helpful to solve these types of problems.