Question

In a solid AB having $NaCl$ structure, A atoms occupy the corners of the cubic unit cell. If all the face-centered atoms along one of the axes are removed, then the resultant stoichiometry of the solid is.
A) $A{B_2}$
B)${A_2}B$
C) ${A_4}{B_3}$
D) ${A_3}{B_4}$

Answer 1

Hint: We know that a unit is the smallest representation of a whole crystal. During a unit, an atom's coordination number is the number of atoms it's touching. The coordination number of face-centered cubic (FCC) is twelve and contains four atoms per unit. The coordination of the body-centered cubic (bcc) is eight and contains two atoms per unit.
Complete step by step answer:
First, we discuss the face centered cubic crystal lattice,
Face centered cubic (FCC):
There are the eight lattice points at each corner of the face centered crystal and there are additional lattice points at the middle of every face of the cube. The given diagram clearly explains how atoms are arranged in FCC.

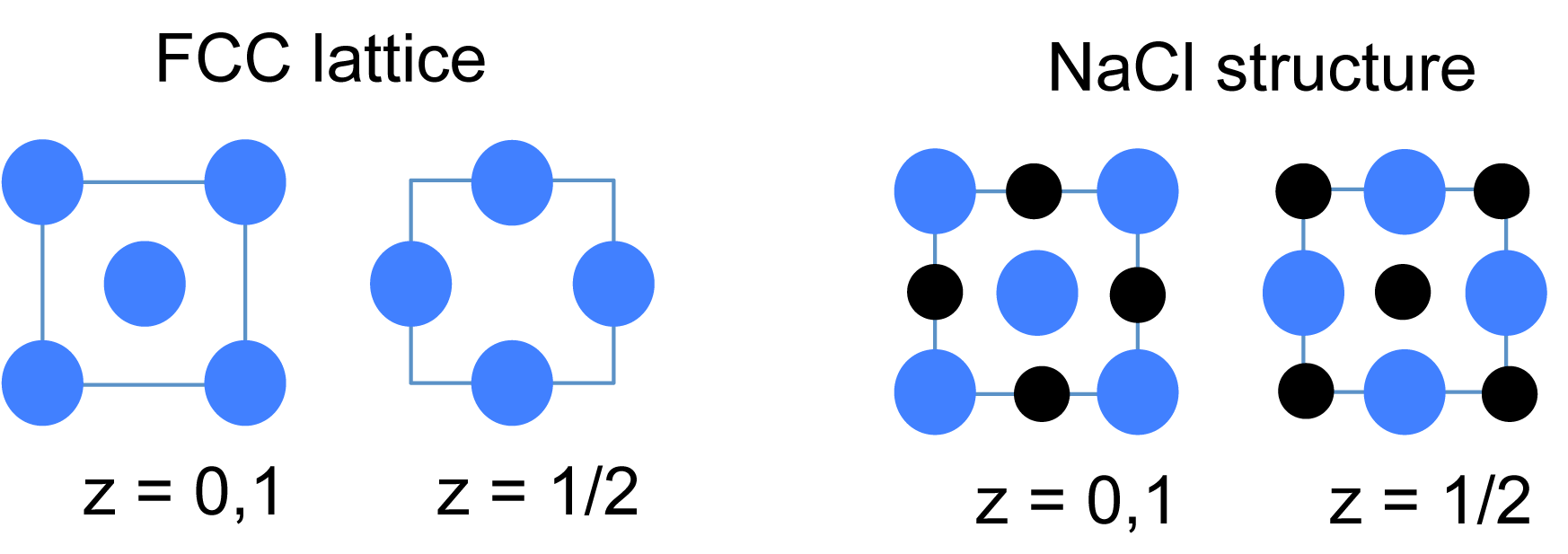
By using the given formula we can easily calculate the fcc of a crystal as,
${\text{FCC}} = \dfrac{{{\text{Total number of edges}}}}{{{\text{Number of atoms share}}}} + \dfrac{{{\text{Number of corners }}}}{{{\text{Number of atoms shared}}}}$
According to the structure of sodium chloride:
Here, A will occupy eight corners of cubic unit cell which will contribute $1/8$ each to the cube therefore \[8 \times {\text{ }}\dfrac{1}{8}{\text{ }} = 1\]and six face centered atoms will contribute $1/2$ to the cube.
Therefore, $6 \times \dfrac{1}{2} = 3$
Thus the total contribution of atom 'A' is \[3 + 1 = 4\]
Now B occupies octahedral voids which contribute \[1/4\].Thus, \[1 + 12 \times {\text{ }}\dfrac{1}{4}{\text{ }} = 4\].The atoms in the face centered crystal are removed from cube is two so contributions from 'A' remains
$8 \times \dfrac{1}{8} + 4 \times \dfrac{1}{2} = 3$ Thus the resultant becomes \[{A_3}{B_4}\].
Therefore option D is correct.


Note:
Don’t get confused between the amount of atoms within the primitive cell and therefore the body center unit cells. The entire number of atoms within the body centered unit is 2. One among the atoms is present at the middle of the middle of the unit whereas the entire number of atoms within the primitive cell is one.