Question

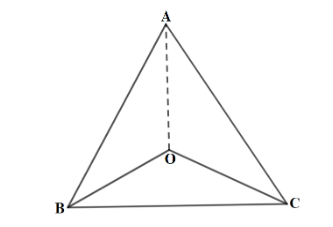
In a triangle ABC, AB=AC and the bisectors of angles B and C intersect at O. Prove that BO=CO and AO is the bisector of angle \[\left| \!{\underline {
  {BAC} }} \right. \].

Answer 1

Hint: Here in this question, we have to prove a side BO=CO using a given isosceles triangle ABC. This can be proven by using some properties of triangles and one of the Criteria for Congruence of Triangles i.e., SAS congruence rule which is one of the postulates and by some further simplification to get the required solution.

Complete step-by-step answer:
Consider a given \[\Delta ABC\], side \[AB = AC\] so it’s a isosceles triangle and the bisectors of angle B and angle C are intersect at point
i.e., \[BO\] and \[CO\] are bisectors of angle \[\left| \!{\underline {
  B }} \right. \] and angle \[\left| \!{\underline {
  C }} \right. \], then
\[ \Rightarrow \left| \!{\underline {
  {ABO} }} \right. = \dfrac{{\left| \!{\underline {
  B }} \right. }}{2}\] and \[\left| \!{\underline {
  {ACO} }} \right. = \dfrac{{\left| \!{\underline {
  C }} \right. }}{2}\].
Therefore, \[\left| \!{\underline {
  {ABO} }} \right. = \dfrac{{\left| \!{\underline {
  B }} \right. }}{2} = \dfrac{{\left| \!{\underline {
  C }} \right. }}{2} = \left| \!{\underline {
  {ACO} }} \right. \]---------(1)
Given, in triangle ABC side \[AB = AC\], then
Angles opposite to equal sides of an isosceles triangle are equal.
\[\therefore AB = AC\]
\[ \Rightarrow \left| \!{\underline {
  C }} \right. = \left| \!{\underline {
  B }} \right. \]
It’s also equals to
\[ \Rightarrow \dfrac{{\left| \!{\underline {
  C }} \right. }}{2} = \dfrac{{\left| \!{\underline {
  B }} \right. }}{2}\]------------(2).
To prove \[BO = CO\], Consider triangle \[\Delta BCO\].
In \[\Delta BCO\],
\[ \Rightarrow \left| \!{\underline {
  {OBC} }} \right. = \left| \!{\underline {
  {OCB} }} \right. \]
Then, the sides opposite to equal angles of a triangle are equal.
\[ \Rightarrow BO = CO\]---------(3)
Hence proved
To prove \[AO\] is the bisector of angle \[\left| \!{\underline {
  {BAC} }} \right. \].
Consider triangles \[\Delta ABO\] and \[\Delta ACO\]. In these two triangles we observed
\[ \Rightarrow AB = AC\] [given in the question]
\[ \Rightarrow BO = CO\] [from equation (3) or proved in last step]
\[ \Rightarrow \left| \!{\underline {
  {ABO} }} \right. = \left| \!{\underline {
  {ACO} }} \right. \] [from equation (1)]
Hence, by SAS postulate i.e., when Two triangles are congruent if two sides and the included angle of one triangle are equal to the two sides and the included angle of the other triangle.
\[ \Rightarrow \Delta ABO \cong \Delta ACO\]
since they are corresponding angles of congruent triangles.
\[ \Rightarrow \left| \!{\underline {
  {BAO} }} \right. = \left| \!{\underline {
  {CAO} }} \right. \]
\[ \Rightarrow AO\] bisects \[\left| \!{\underline {
  A }} \right. \]
Hence, proved

Note: While solving these type of questions, we have to know the some basic properties, Axiom and postulates of triangle like when two triangles are congruent all sides and angles of two triangles should be equal, when if two triangles are similar the corresponding sides are in proportion and the corresponding angles are congruent and know about postulates like SAS, ASA, AAA etc…