Question

In an equilateral triangle , the inradius, circumradius, and one of the ex –radii are
In the ratio
$
  {\text{A}}{\text{. 2:3:5}} \\
  {\text{B}}{\text{. 1:2:3}} \\
  {\text{C}}{\text{. 1:3:7}} \\
  {\text{D}}{\text{. 3:7:9}} \\
$

Answer 1

Hint: To solve this question we have to have knowledge of inradius circumradius and ex-radius and then using the property of the solution of the triangle we have to find their ratio. And also keep in mind it is an equilateral triangle so all sides are the same.

Complete step-by-step answer:
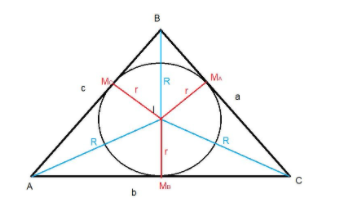
We have given a equilateral triangle and we know inradius is denoted by ‘r’ and circumradius is denoted by ‘R’ and one of the ex-radius is ${r_1}$
We have to find $r:R:{r_1}$
Now we know,
Area of equilateral triangle =$\dfrac{{\sqrt 3 }}{4}{a^2}$
Perimeter of equilateral triangle = 3a =2s, $\therefore s = \dfrac{{3a}}{2}$
Now using the properties of solution of triangle
$r = \dfrac{\Delta }{s} = \dfrac{{\dfrac{{\sqrt 3 }}{4}{a^2}}}{{\dfrac{{3a}}{2}}} = \dfrac{a}{{2\sqrt 3 }}$
Now we know
$R = \dfrac{{abc}}{{4\Delta }}$ and here equilateral triangle triangle is given so a = b = c
$\therefore R = \dfrac{{{a^3}}}{{4 \times \dfrac{{\sqrt 3 }}{4}{a^2}}} = \dfrac{a}{{\sqrt 3 }}$
And we also know
${r_1} = \dfrac{\Delta }{{s - a}} = \dfrac{{\dfrac{{\sqrt 3 }}{4}{a^2}}}{{\dfrac{{3a}}{2} - a}} = \dfrac{{\sqrt 3 }}{4}{a^2} \times \dfrac{2}{a} = \dfrac{{\sqrt 3 }}{2}a$
Now we have
$r = \dfrac{a}{{2\sqrt 3 }},R = \dfrac{a}{{\sqrt 3 }},{r_1} = \dfrac{{\sqrt 3 }}{2}a$
So we have to find ratio of all these three
$r:R:{r_1} = \dfrac{a}{{2\sqrt 3 }}:\dfrac{a}{{\sqrt 3 }}:\dfrac{{\sqrt 3 }}{2}a$
On simplifying this we get,
1:2:3
Hence option B is the correct option.

Note: Whenever we get this type of question the key concept of solving is we should have remembered all this formulae ${r_1} = \dfrac{\Delta }{{s - a}},R = \dfrac{{abc}}{{4\Delta }},2s = {\text{perimeter}}$ then we can solve easily this question.