Question

In \[\Delta ABC\text{ AB=20cm, BC=21cm and AC=29cm}\] find the radius of the circle touching all the sides of \[\Delta ABC.\]

Answer 1

Hint: We know that a circle that touches all the sides of a triangle is known as incircle and its radius is known as inradius, denoted by 'r' and the value of inradius is equal to the ratio of area of triangles to semi perimeter of the triangle. Mathematically, \[r=\dfrac{\Delta }{S}\] where \[\Delta \] is the area and S is a semi perimeter.

Complete step-by-step answer:
Also, we will use the heron's formula to calculate the area of a triangle having sides a, b and c given by,
\[\Delta =\sqrt{S\left( S-a \right)\left( S-b \right)\left( S-c \right)}\]
Where, \[S=\dfrac{a+b+c}{2}\]

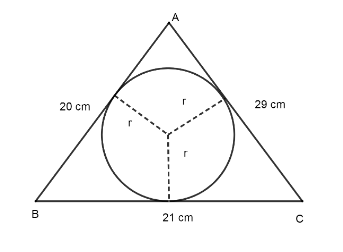
We have been given the side of a \[\Delta ABC\text{ AB=20cm, BC=21cm and AC=29cm}\] and asked to find the radius of the circle touching all the sides of \[\Delta ABC.\]
We know that a circle that touches all the side of \[\Delta ABC\] is known as incircle and in radius is known as inradius, denoted by 'r' and given by,
\[r=\dfrac{\Delta }{S}\]
Where,\[\Delta =\text{area of triangle = }\sqrt{S\left( S-a \right)\left( S-b \right)\left( S-c \right)}\]. Now known as Heron's formula.
\[S=\text{ semi-perimeter = }\dfrac{a+b+c}{2}\]
a, b and c are sides of the triangle.
We have \[\text{AB=20cm, BC=21cm and AC=29cm}\]
\[\Rightarrow S=\dfrac{20+21+29}{2}=\dfrac{70}{2}=35cm.\]
So,
 \[\begin{align}
  & \Delta =\sqrt{35\left( 35-20 \right)\left( 35-21 \right)\left( 35-29 \right)} \\
 & \text{ = }\sqrt{35\times 15\times 14\times 6} \\
 & \text{ = }\sqrt{44100} \\
 & \text{ = 210 c}{{\text{m}}^{\text{2}}} \\
\end{align}\]
Now, the inradius (r) \[\Rightarrow \dfrac{\Delta }{S}\]
\[\begin{align}
  & \Rightarrow \dfrac{210}{35} \\
 & \Rightarrow 6cm \\
\end{align}\]
Therefore, the radius of the circle that touches all the sides of \[\Delta ABC\] is equal to 6cm.

Note: First of all be careful while calculating the value of semi perimeter i.e. S as sometimes we just add all the sides of the triangle and forget to divide it by 2 and we get the incorrect answer.Also, you can observe that the given triangle has a right angled triangle so the inradius of the triangle is \[r=\dfrac{P+B+H}{2}\] where, P, B and H have their own meaning. This concept is very important in the competitive examination view as it will save your time.