
In each pair of triangles in the following figure, parts bearing identical marks are congruent .State the test and correspondence of vertices by which triangles in each pair are congruent
\[(a)\]
\[(b)\]
\[(c)\]
\[(d)\]
\[(e)\]
\[(f)\]






Answer
498.3k+ views
Hint: In this question we need to check the conditions of two triangles to be congruent. Basically there are five conditions for two triangles to be congruent they are \[\text{SSS(side side side)}\] , \[\text{SAS(side angle side)}\] , \[\text{ASA(angle side angle)}\] , \[\text{AAS(angle angle side)}\] and \[\text{RHS(right angle-hypotenuse-side)}\] .
Complete answer:
The triangles are said to be congruent if they are of the same shape and size. We may represent the congruence by the symbol \[\widetilde{\text{=}}\] . If the two triangles are congruent then their parameters and areas are equal.
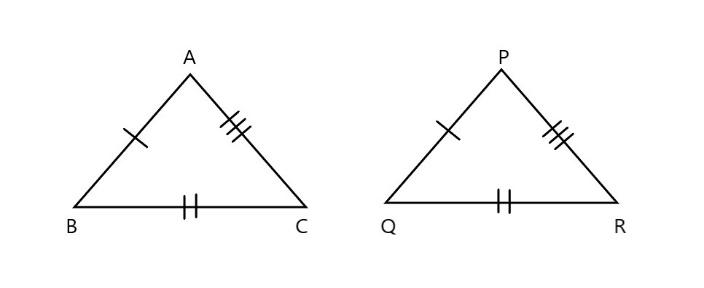
\[\text{(a)}\]
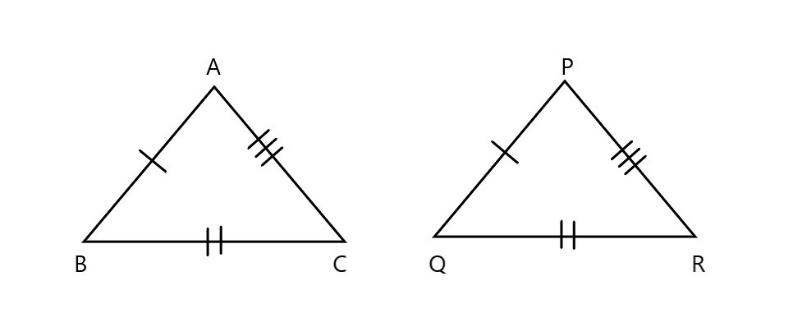
In the above figure in the given \[\vartriangle ABC\] and \[\vartriangle PQR\]
\[\text{AB=PQ}\] \[\text{(}\] corresponding sides are equal \[\text{)}\]
\[\text{AC=QR}\] \[\text{(}\] corresponding sides are equal \[\text{)}\]
\[\text{QC=PR}\] \[\text{(}\] corresponding sides are equal \[\text{)}\]
Here all the corresponding sides are equal in length. Hence it follows \[\text{SSS (side side side)}\] property.
THUS, we can say that \[\vartriangle ABC\widetilde{=}\vartriangle PQR\]
\[\text{(b)}\]
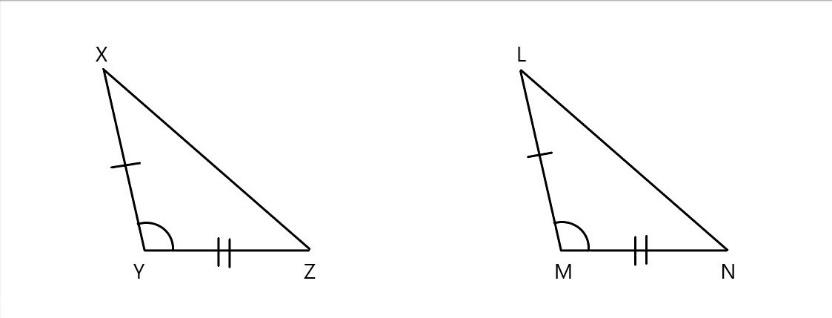
In the above figure in the given \[\vartriangle XYZ\] and \[\vartriangle LMN\]
\[\angle \text{Y=}\angle \text{M}\] \[\text{(}\] corresponding angles are equal \[\text{)}\]
\[XY=LM\] \[\text{(}\] corresponding sides are equal \[\text{)}\]
\[YZ=MN\] \[\text{(}\] corresponding sides are equal \[\text{)}\]
Here all the corresponding sides are equal in length. Hence it follows \[\text{SAS ( side angle side)}\] property.
THUS, we can say that \[\vartriangle \text{XYZ}\widetilde{=}\vartriangle LMN\]
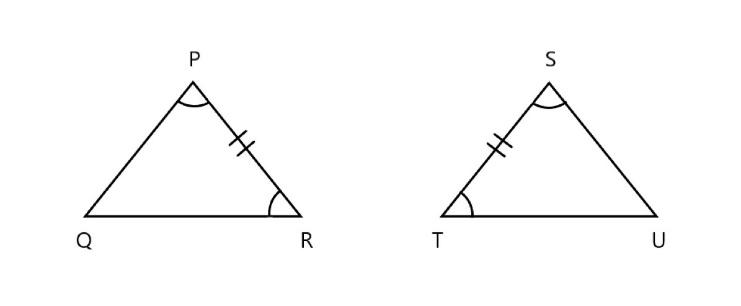
\[\text{(c)}\]
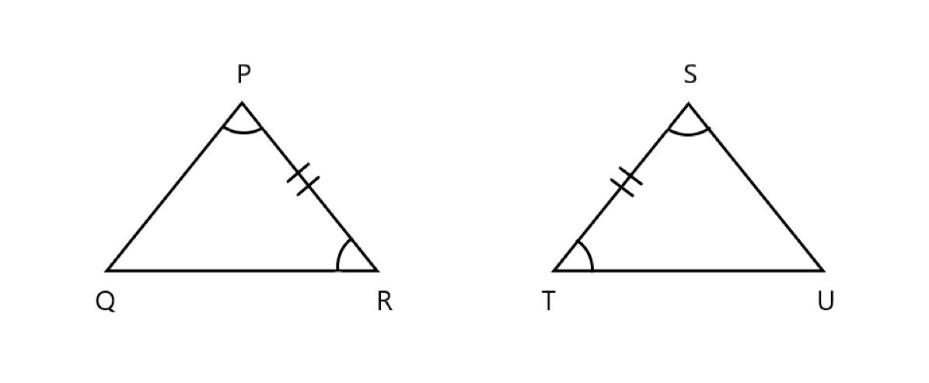
In the above figure in \[\vartriangle PQR\] and \[\vartriangle STU\]
\[\vartriangle \text{QPR=}\vartriangle T\text{SU}\] \[\text{(}\] corresponding angles are equal \[\text{)}\]
\[\text{PR=ST}\] \[\text{(}\] corresponding sides are equal \[\text{)}\]
\[\vartriangle \text{QRP=}\vartriangle T\text{US}\] \[\text{(}\] corresponding angles are equal \[\text{)}\]
Here all the corresponding sides are equal in length. Hence it follows \[\text{ASA (angle side angle)}\] property.
THUS, we can say that \[~\vartriangle PQR\widetilde{=}\vartriangle STU\]
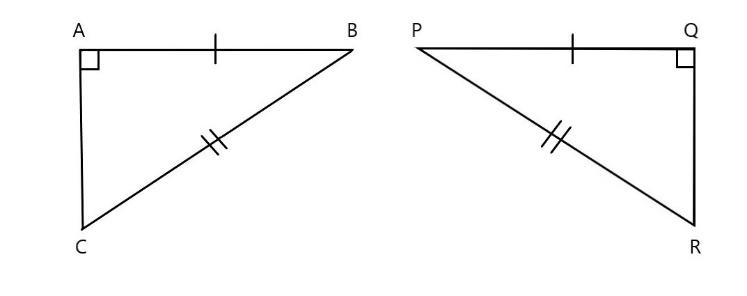
\[\text{(d)}\]
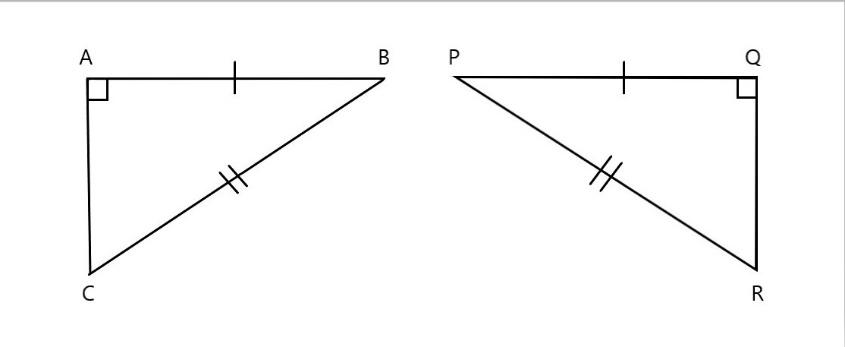
In the above figure in the given \[\vartriangle BAC\] and \[\vartriangle PQR\]
\[\vartriangle BAC~=\vartriangle PQR\] \[\text{(}\] corresponding angles are right angle \[\text{)}\]
\[\text{AB=PQ}\] \[\text{(}\] corresponding sides are equal \[\text{)}\]
\[\text{BC=PR}\] \[\text{(}\] corresponding sides are equal \[\text{)}\]
Here all the corresponding sides are equal in length. Hence it follows \[\text{RHS (right angle- hypotenuse side)}\] property.
Thus, we can say that \[\vartriangle BAC~\widetilde{=}\vartriangle PQR\]
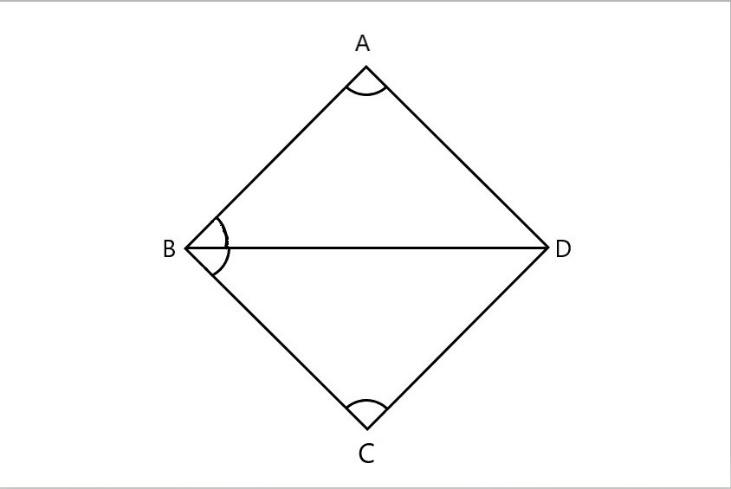
\[\text{(e)}\]
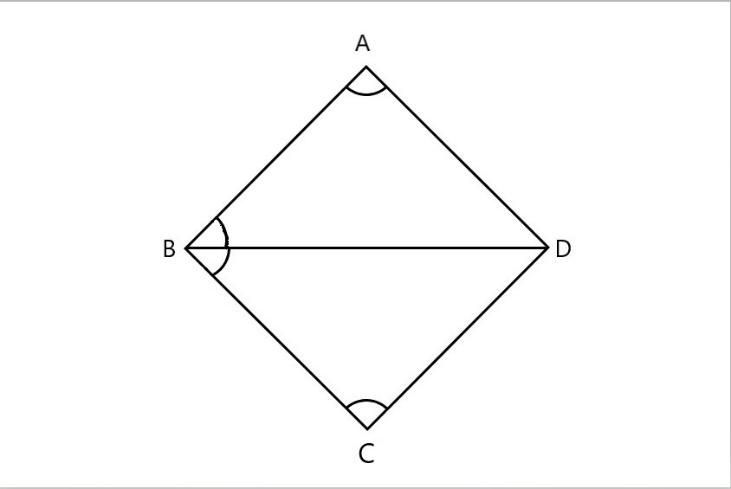
In the above figure in the given \[\vartriangle DAB\] and \[\vartriangle DCB\]
\[\vartriangle DAB=\vartriangle DCB\] \[\text{(}\] corresponding angles are equal \[\text{)}\]
\[\vartriangle ABD\text{=}\vartriangle BCD\] \[\text{(}\] corresponding angles are equal \[\text{)}\]
\[\text{BD=BD}\] \[\text{(}\] common lines \[\text{)}\]
Here all the corresponding sides are equal in length. Hence it follows \[\text{ASA (angle side angle)}\] property.
Thus, we can say that \[\vartriangle DAB\widetilde{=}\vartriangle DCB\]
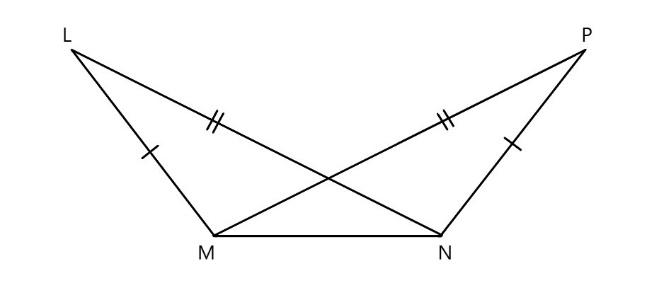
\[\text{(f)}\]
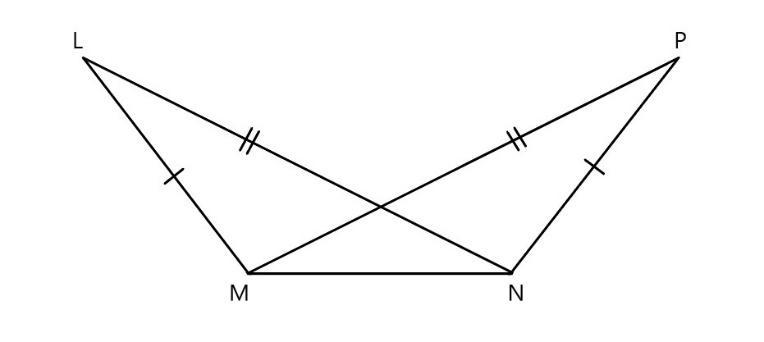
In the above figure in the given \[\vartriangle LMN\widetilde{=}\vartriangle PNM\]
\[\text{LM=PN}\] \[\text{(}\] corresponding sides are equal \[\text{)}\]
\[\text{LN=PM}\] \[\text{(}\] corresponding sides are equal \[\text{)}\]
\[\text{MN=MN}\] \[\text{(}\] common line \[\text{)}\]
Here all the corresponding sides are equal in length. Hence it follows \[\text{SSS (side side side)}\] property.
THUS, we can say that \[\vartriangle LMN\widetilde{=}\vartriangle PNM\] .
Note:
\[\text{SSA(side side angle) }\] does not follow congruence property because the unknown side could be located in two different places and \[\text{AAA(angle angle angle)}\] also not follows the congruence property as both the triangles may be similar but they are not congruent.
Complete answer:
The triangles are said to be congruent if they are of the same shape and size. We may represent the congruence by the symbol \[\widetilde{\text{=}}\] . If the two triangles are congruent then their parameters and areas are equal.
\[\text{(a)}\]

In the above figure in the given \[\vartriangle ABC\] and \[\vartriangle PQR\]
\[\text{AB=PQ}\] \[\text{(}\] corresponding sides are equal \[\text{)}\]
\[\text{AC=QR}\] \[\text{(}\] corresponding sides are equal \[\text{)}\]
\[\text{QC=PR}\] \[\text{(}\] corresponding sides are equal \[\text{)}\]
Here all the corresponding sides are equal in length. Hence it follows \[\text{SSS (side side side)}\] property.
THUS, we can say that \[\vartriangle ABC\widetilde{=}\vartriangle PQR\]
\[\text{(b)}\]

In the above figure in the given \[\vartriangle XYZ\] and \[\vartriangle LMN\]
\[\angle \text{Y=}\angle \text{M}\] \[\text{(}\] corresponding angles are equal \[\text{)}\]
\[XY=LM\] \[\text{(}\] corresponding sides are equal \[\text{)}\]
\[YZ=MN\] \[\text{(}\] corresponding sides are equal \[\text{)}\]
Here all the corresponding sides are equal in length. Hence it follows \[\text{SAS ( side angle side)}\] property.
THUS, we can say that \[\vartriangle \text{XYZ}\widetilde{=}\vartriangle LMN\]
\[\text{(c)}\]

In the above figure in \[\vartriangle PQR\] and \[\vartriangle STU\]
\[\vartriangle \text{QPR=}\vartriangle T\text{SU}\] \[\text{(}\] corresponding angles are equal \[\text{)}\]
\[\text{PR=ST}\] \[\text{(}\] corresponding sides are equal \[\text{)}\]
\[\vartriangle \text{QRP=}\vartriangle T\text{US}\] \[\text{(}\] corresponding angles are equal \[\text{)}\]
Here all the corresponding sides are equal in length. Hence it follows \[\text{ASA (angle side angle)}\] property.
THUS, we can say that \[~\vartriangle PQR\widetilde{=}\vartriangle STU\]
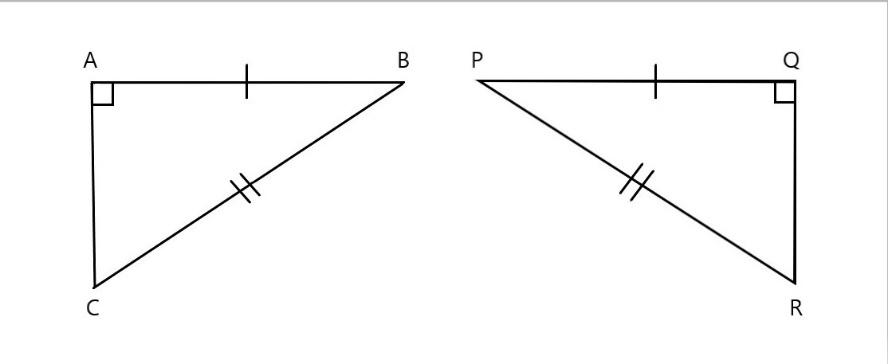
\[\text{(d)}\]

In the above figure in the given \[\vartriangle BAC\] and \[\vartriangle PQR\]
\[\vartriangle BAC~=\vartriangle PQR\] \[\text{(}\] corresponding angles are right angle \[\text{)}\]
\[\text{AB=PQ}\] \[\text{(}\] corresponding sides are equal \[\text{)}\]
\[\text{BC=PR}\] \[\text{(}\] corresponding sides are equal \[\text{)}\]
Here all the corresponding sides are equal in length. Hence it follows \[\text{RHS (right angle- hypotenuse side)}\] property.
Thus, we can say that \[\vartriangle BAC~\widetilde{=}\vartriangle PQR\]
\[\text{(e)}\]

In the above figure in the given \[\vartriangle DAB\] and \[\vartriangle DCB\]
\[\vartriangle DAB=\vartriangle DCB\] \[\text{(}\] corresponding angles are equal \[\text{)}\]
\[\vartriangle ABD\text{=}\vartriangle BCD\] \[\text{(}\] corresponding angles are equal \[\text{)}\]
\[\text{BD=BD}\] \[\text{(}\] common lines \[\text{)}\]
Here all the corresponding sides are equal in length. Hence it follows \[\text{ASA (angle side angle)}\] property.
Thus, we can say that \[\vartriangle DAB\widetilde{=}\vartriangle DCB\]
\[\text{(f)}\]

In the above figure in the given \[\vartriangle LMN\widetilde{=}\vartriangle PNM\]
\[\text{LM=PN}\] \[\text{(}\] corresponding sides are equal \[\text{)}\]
\[\text{LN=PM}\] \[\text{(}\] corresponding sides are equal \[\text{)}\]
\[\text{MN=MN}\] \[\text{(}\] common line \[\text{)}\]
Here all the corresponding sides are equal in length. Hence it follows \[\text{SSS (side side side)}\] property.
THUS, we can say that \[\vartriangle LMN\widetilde{=}\vartriangle PNM\] .
Note:
\[\text{SSA(side side angle) }\] does not follow congruence property because the unknown side could be located in two different places and \[\text{AAA(angle angle angle)}\] also not follows the congruence property as both the triangles may be similar but they are not congruent.
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is pollution? How many types of pollution? Define it

What is the Full Form of ISI and RAW




