Question

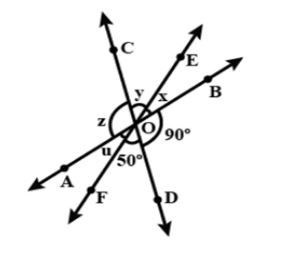
In Fig, three coplanar lines intersect at a point $O$, forming angles as shown in the figure. Find the values of $x, y, z$ and $u$.

Answer 1

Hint: Here, we are given three coplanar lines and having a common intersecting point O. We are given two angles and the remaining four angles need to be found out. Also, we will use one property i.e. vertically opposite angles are equal. And, all the angles on the same line (i.e. on a straight line) have angles equal to 180 degree. So, using all these, we will get our final output.

Complete step by step answer:
Given that, point O is the intersection point of the three coplanar lines.
Also, from the given figure, it is given that,
\[\angle BOD = {90^ \circ }\] and \[\angle DOF = {50^ \circ }\]
We know that, the lines that lie on the same plane are called coplanar lines. Since, we know that, vertically opposite angles are equal.
This means,
1)\[\angle BOD = {90^ \circ }\]
\[ \Rightarrow \angle BOD = \angle AOC\] (Both are vertically opposite angles)
\[ \Rightarrow \angle AOC = z = {90^ \circ }\]
And,
2)\[\angle DOF = {50^ \circ }\]
\[ \Rightarrow \angle DOF = \angle COE\] (Both are vertically opposite angles)
\[ \Rightarrow \angle COE = y = {50^ \circ }\]

Next, according to the given figure, COD is a line, then
\[ \Rightarrow \angle COF + \angle AOF + \angle FOD = {180^ \circ }\] (As they are linear pair)
Substituting the variables, we will get,
\[ \Rightarrow z + u + \angle FOD = {180^ \circ }\]
Putting the values we know, we will get,
\[ \Rightarrow {90^ \circ } + u + {50^ \circ } = {180^ \circ }\]
On simplifying this, we will get,
\[ \Rightarrow {140^ \circ } + u = {180^ \circ }\]
By using transposing method, we will move the term from LHS to RHS, we will get,
\[ \Rightarrow u = {180^ \circ } - {140^ \circ }\]
\[ \Rightarrow u = {40^ \circ }\]
Last, from figure, we can see that, AOB is a line, then,
\[ \Rightarrow \angle BOE + \angle EOC + \angle COA = {180^ \circ }\]
Substitute this values, we will get,
\[ \Rightarrow x + y + z = {180^ \circ }\]
Using the same way, we will get the value of x.
Another Method:
Since, angle AOF = angle EOB
So, \[u = x = {40^ \circ }\]

Hence, the values of all are: \[x = {40^ \circ }\] , \[y = {50^ \circ }\] , \[z = {90^ \circ }\] and \[u = {40^ \circ }\].

Note: Here, students should remember that, x + y + z+ u + 50° + 90° = 360° and so with this, we can check the answers. Also, we know that vertically opposite angles are equal. In short, any two intersecting lines must lie in the same plane, and therefore be coplanar.