
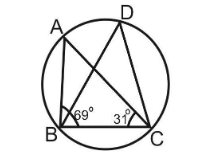
In figure

Answer
485.1k+ views
1 likes
Hint: Here, to find the value of
Complete step-by-step answer:
Here, it is given that
Now, in triangle ABC, by angle sum property of triangle we have
Substituting values in above equation. We have,
Also, we know that in a circle angle subtended by a chord on the same arc of a circle are equal.
Hence, from the figure we see that
But, the value of
Hence, from above we see that the required value of
Note: From the figure we see that chord BC subtends two angles on the arc of the circle. Let the value of
Complete step-by-step answer:
Here, it is given that
Now, in triangle ABC, by angle sum property of triangle we have
Substituting values in above equation. We have,
Also, we know that in a circle angle subtended by a chord on the same arc of a circle are equal.
Hence, from the figure we see that
But, the value of
Hence, from above we see that the required value of
Note: From the figure we see that chord BC subtends two angles on the arc of the circle. Let the value of
Latest Vedantu courses for you
Grade 10 | CBSE | SCHOOL | English
Vedantu 10 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What is pollution? How many types of pollution? Define it




