Question

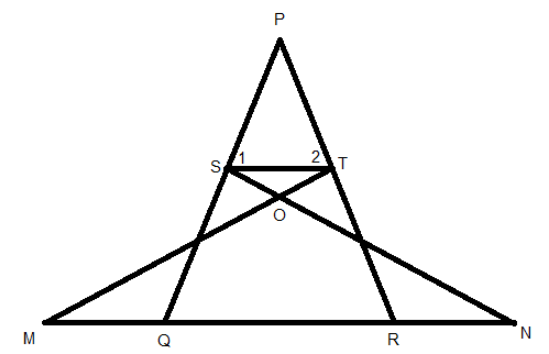
In given figure $\angle 1 = \angle 2$ and $\Delta NSQ \cong \Delta MTR$ , then prove that $\Delta PTS \sim \Delta PRQ$

Answer 1

Hint:
We can equate the corresponding sides of congruent triangles. Then we can equate the sides opposite to equal angles in a triangle. From these two relations, we can show that 2 sides are proportional. Then we can take the common angle of the triangles. Using these conditions, we can prove the required triangles are similar.

Complete step by step solution:
Consider the triangle PST,
It is given that $\angle 1 = \angle 2$ .
We know that in a triangle, the sides opposite to equal angles will be equal.
So, from the figure, we can write,
 $PT = PS$ … (1)
It is given that $\Delta NSQ \cong \Delta MTR$ .
We know that corresponding sides of congruent triangles are equal.
 $ \Rightarrow SQ = TR$ .. (2).
Now we can add equations (2) and (1).
 $ \Rightarrow PS + SQ = PT + TR$
From the figure, we can write,
 $ \Rightarrow PQ = PR$ .. (3)
Now we can consider the triangles PTS and PRQ.
We can consider the angles \[\angle SPT\] and \[\angle QPR\] .
From the figure, they represent the same angles. So, they will be equal.
 \[ \Rightarrow \angle SPT = \angle QPR\]
Now consider the sides PS and PQ. We can take their ratio.
 \[ \Rightarrow \dfrac{{PS}}{{PQ}}\]
Now we can apply equations (1) and (3). Then we get,
  \[ \Rightarrow \dfrac{{PS}}{{PQ}} = \dfrac{{PT}}{{PR}}\]
So, the 2 sides are proportional.
As the 2 sides are proportional and the corresponding angle between them are equal, we can say that the triangles PTS and PRS are similar.
So, we get, $\Delta PTS \sim \Delta PRQ$
Hence proved.

Note:
Note: Alternate solution is given by,
 Consider the triangle PST,
It is given that $\angle 1 = \angle 2$ .
We know that in a triangle, the sides opposite to equal angles will be equal.
So, from the figure, we can write,
 $PT = PS$ … (a)
It is given that $\Delta NSQ \cong \Delta MTR$ .
We know that corresponding sides of congruent triangles are equal.
 $ \Rightarrow SQ = TR$ .. (b).
Now we can add equations (a) and (b).
 $ \Rightarrow PS + SQ = PT + TR$
From the figure, we can write,
 $ \Rightarrow PQ = PR$ .. (c)
PQ and PR are sides of the triangle PQR and are equal. Then the opposite angles will be equal.
 $ \Rightarrow \angle PQR = \angle PRQ$ … (d)
Consider the triangles PTS and PRQ
By taking the angle sum property we get,
 $ \Rightarrow 180^\circ = \angle P + \angle 1 + \angle 2$
On rearranging and applying the given condition, we get,
 $ \Rightarrow 180^\circ - \angle P = 2\angle 1$ … (e)
 $ \Rightarrow 180^\circ = \angle P + \angle PQR + \angle PRQ$
On rearranging and substituting (d), we get
 $ \Rightarrow 180^\circ - \angle P = 2\angle PQR$ … (f)
On comparing (e) and (f), we get,
 $ \Rightarrow \angle 1 = \angle PQR$
On substituting, equation (d) and given condition, we get,
 $ \Rightarrow \angle 2 = \angle PRQ$
Now we can consider the triangles PTS and PRQ.
We can consider the angles \[\angle SPT\] and \[\angle QPR\] .
From the figure, they represent the same angles. So, they will be equal.
 \[ \Rightarrow \angle SPT = \angle QPR\]
From the above results, we can write,
 $ \Rightarrow \angle 1 = \angle PQR$
 $ \Rightarrow \angle 2 = \angle PRQ$
As the corresponding angles are equal, we can say that the triangles PTS and PRS are similar.
So, we get, $\Delta PTS \sim \Delta PRQ$
Hence proved.