Question

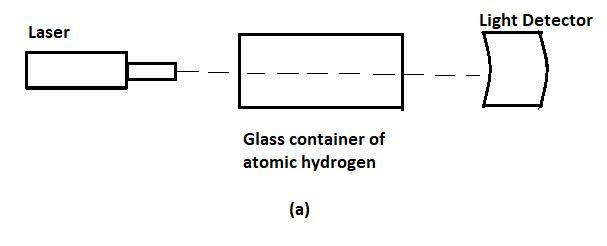
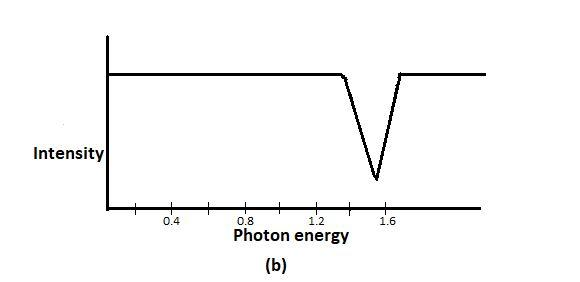
In order to determine the value of ${{E}_{0}}$, a scientist shines photons (“light particles”) of various energies at a cloud of atomic hydrogen. Most of the hydrogen atoms occupy the ground state. A detector records the intensity of light transmitted through that cloud; as shown in the figure above. The graph in the above figure is that of part of the scientist’s data, showing the intensity of the transmitted light as a function of the photon energy. A hydrogen atom electron is likely to absorb a photon only if the photon gives the electron enough energy to knock it into a higher shell.
According to this experiment, what is the approximate value of ${{E}_{0}}$?

A.$1.6\times {{10}^{-18}}J$
B.$2.1\times {{10}^{-18}}J$
C.$3.2\times {{10}^{-18}}J$
D.$6.4\times {{10}^{-18}}J$

Answer 1

Hint: In this question, we find the approximate value of ${{E}_{0}}$ according to the experiment. We use Bohr’s model for solving this question. We find the energy on the first and second excitation energy. Then take the difference between them to find out the value of ${{E}_{0}}$.

Complete answer:
Given:
Photon energy \[=1.6\times {{10}^{-18}}J\]
From figure b photon energy $1.6\times {{10}^{-18}}J$ gets absorbed in large numbers, no lower energy photon gets absorbed, and according to the passage, substantial absorption occurs only if the photon jumps the ground-state electron into a higher shell.
So, $1.6\times {{10}^{-18}}J$ photon knocks a ground-state electron ($n=1$) into the first excited state ($n=2$). So, the difference in energy between the ground and the first excited state must be $1.6\times {{10}^{-18}}J$.
Using the below equation
${{E}_{n}}=\dfrac{{{E}_{0}}}{{{n}^{2}}}$
Now we find the energy for \[{{E}_{1}}\]
 \[{{E}_{1}}=\dfrac{{{E}_{0}}}{{{1}^{2}}}\]
Now we find the energy for ${{E}_{2}}$
 \[{{E}_{2}}=\dfrac{{{E}_{0}}}{{{2}^{2}}}\]
Now we substitute ${{E}_{1}}$ from ${{E}_{2}}$ then we get,
$1.6\times {{10}^{-18}}={{E}_{2}}-{{E}_{1}}$
We have the values of the ${{E}_{1}}$ and ${{E}_{2}}$ so we put these values in the below equation
$\begin{align}
  & 1.6\times {{10}^{-18}}=-\dfrac{{{E}_{0}}}{4}-(\dfrac{-{{E}_{0}}}{1}) \\
 & \\
\end{align}$
After simplifying this equation we get,
$1.6\times {{10}^{-18}}=\dfrac{3}{4}{{E}_{0}}$
Then,
${{E}_{0}}=\dfrac{4}{3}(1.6\times {{10}^{-18}})$
After solving this we get,
${{E}_{0}}=2.1\times {{10}^{-18}}J$
Here is the value of the ${{E}_{0}}$ according to the experiment.

So option B is correct.

Note:
To solve this question students know the energy states and Bohr's model. Bohr model depicts an atom as a small, positively charged nucleus surrounded by electrons. These electrons travel in circular orbits around the nucleus, similar in structure to the solar system, except electrostatic forces rather than gravity provide attraction. If an atom, ion, or molecule is at the lowest possible energy level, it and its electrons are said to be in the ground state. If it is at a higher energy level, it is said to be excited, or any electrons that have higher energy than the ground state are excited. After learning about these terms you can easily solve this type of question.