
In refraction incident ray and emergent ray are parallel. Type 1 for true and 0 for false.
Answer
124.5k+ views
Hint: To answer this question, we need to take the case of refraction through a glass slab. Then we need to examine whether the emergent ray is parallel to the incident ray, using Snell's law.
Formula Used: The formula used in this solution is
\[\mu = \dfrac{{\sin i}}{{\sin r}}\], \[\mu = \]refractive index, \[i = \]angle of incidence, and \[r = \] angle of refraction
Complete step-by-step answer
Consider a glass slab of refractive index \[\mu \] as shown in the flowing figure.
A ray \[AB\] is incident on the upper interface at the point \[C\], which gets refracted in the glass medium as the ray \[CD\]. The refracted ray is incident on the lower interface at the point \[E\]. Finally, \[CD\] is refracted and emerges out of the glass medium back into the air as the ray\[EF\].
Applying Snell’s law on the upper interface, we get
\[\mu = \dfrac{{\sin i}}{{\sin r}}\] (i)
Again applying Snell’s law on the lower interface, we get
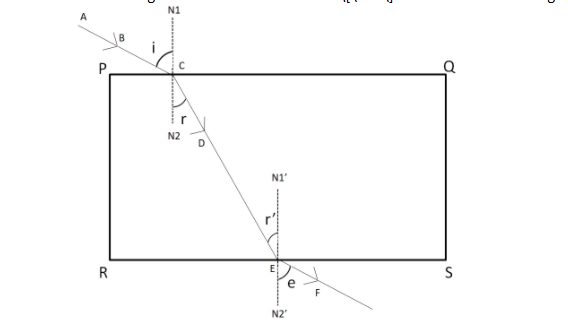
\[\mu = \dfrac{{\sin e}}{{\sin r'}}\] (ii)
As \[{N_1}{N_2}\] is the normal to the upper interface,
\[\therefore {N_1}{N_2} \bot PQ\] (iii)
Also, \[{N’_1}{N’_2}\] is the normal to the lower surface
\[\therefore {N’_1}{N’_2} \bot RS\] (iv)
Case 1
If \[PQ\parallel RS\] then by (iii) and (iv), we have
\[{N_1}{N_2}\parallel {N’_1}{N’_2}\]
Now, in the figure, as \[r\] and \[r'\] are alternate interior angles, so they are equal.
\[\therefore r = r'\]
Taking sine both the sides, we get
\[\sin r = \sin r'\] (v)
From (i) and (ii)
\[\dfrac{{\sin i}}{{\sin r}} = \dfrac{{\sin e}}{{\sin r'}}\]
Multiplying with \[\sin r\] on both sides
\[\sin i = \sin r\dfrac{{\sin e}}{{\sin r'}}\]
From (v)
\[\sin i = \sin e\]
\[\because \] both \[i\& e\] are acute, so we can say
\[i = e\]
As \[{N_1}{N_2} \parallel {N’_1}{N’_2}\] and \[i = e\]
So \[AB\parallel EF\]
Hence, the incident ray and emergent ray are parallel.
Case 2
If \[PQ\& RS\] are not parallel, then
\[r \ne r'\]
both \[i\& e\] are acute, so we can say
\[\sin r \ne \sin r'\]
From (i) and (ii)
\[\dfrac{{\sin i}}{{\sin r}} = \dfrac{{\sin e}}{{\sin r'}}\]
But \[\sin r \ne \sin r'\]
So, \[\sin i \ne \sin e\] and therefore
\[i \ne e\]
Thus, \[AB\] is not parallel to \[EF\]
\[\therefore \] We conclude that the incident and the emergent rays are parallel only with the condition that the two refracting interfaces should be parallel to each other. They are not always parallel.
So the statement given in the question is false.
Hence, the correct answer is 0.
Note: This question can also be attempted by taking the case of refraction through a triangular prism. In that case, we can directly conclude that the emergent ray is not parallel to the incident ray through simple observation.
Formula Used: The formula used in this solution is
\[\mu = \dfrac{{\sin i}}{{\sin r}}\], \[\mu = \]refractive index, \[i = \]angle of incidence, and \[r = \] angle of refraction
Complete step-by-step answer
Consider a glass slab of refractive index \[\mu \] as shown in the flowing figure.
A ray \[AB\] is incident on the upper interface at the point \[C\], which gets refracted in the glass medium as the ray \[CD\]. The refracted ray is incident on the lower interface at the point \[E\]. Finally, \[CD\] is refracted and emerges out of the glass medium back into the air as the ray\[EF\].
Applying Snell’s law on the upper interface, we get
\[\mu = \dfrac{{\sin i}}{{\sin r}}\] (i)
Again applying Snell’s law on the lower interface, we get

\[\mu = \dfrac{{\sin e}}{{\sin r'}}\] (ii)
As \[{N_1}{N_2}\] is the normal to the upper interface,
\[\therefore {N_1}{N_2} \bot PQ\] (iii)
Also, \[{N’_1}{N’_2}\] is the normal to the lower surface
\[\therefore {N’_1}{N’_2} \bot RS\] (iv)
Case 1
If \[PQ\parallel RS\] then by (iii) and (iv), we have
\[{N_1}{N_2}\parallel {N’_1}{N’_2}\]
Now, in the figure, as \[r\] and \[r'\] are alternate interior angles, so they are equal.
\[\therefore r = r'\]
Taking sine both the sides, we get
\[\sin r = \sin r'\] (v)
From (i) and (ii)
\[\dfrac{{\sin i}}{{\sin r}} = \dfrac{{\sin e}}{{\sin r'}}\]
Multiplying with \[\sin r\] on both sides
\[\sin i = \sin r\dfrac{{\sin e}}{{\sin r'}}\]
From (v)
\[\sin i = \sin e\]
\[\because \] both \[i\& e\] are acute, so we can say
\[i = e\]
As \[{N_1}{N_2} \parallel {N’_1}{N’_2}\] and \[i = e\]
So \[AB\parallel EF\]
Hence, the incident ray and emergent ray are parallel.
Case 2
If \[PQ\& RS\] are not parallel, then
\[r \ne r'\]
both \[i\& e\] are acute, so we can say
\[\sin r \ne \sin r'\]
From (i) and (ii)
\[\dfrac{{\sin i}}{{\sin r}} = \dfrac{{\sin e}}{{\sin r'}}\]
But \[\sin r \ne \sin r'\]
So, \[\sin i \ne \sin e\] and therefore
\[i \ne e\]
Thus, \[AB\] is not parallel to \[EF\]
\[\therefore \] We conclude that the incident and the emergent rays are parallel only with the condition that the two refracting interfaces should be parallel to each other. They are not always parallel.
So the statement given in the question is false.
Hence, the correct answer is 0.
Note: This question can also be attempted by taking the case of refraction through a triangular prism. In that case, we can directly conclude that the emergent ray is not parallel to the incident ray through simple observation.
Recently Updated Pages
Young's Double Slit Experiment Step by Step Derivation

Difference Between Circuit Switching and Packet Switching

Difference Between Mass and Weight

JEE Main Participating Colleges 2024 - A Complete List of Top Colleges

JEE Main Maths Paper Pattern 2025 – Marking, Sections & Tips

Sign up for JEE Main 2025 Live Classes - Vedantu

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility & More

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

The formula of the kinetic mass of a photon is Where class 12 physics JEE_Main

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Keys & Solutions

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Main Login 2045: Step-by-Step Instructions and Details

Dual Nature of Radiation and Matter Class 12 Notes: CBSE Physics Chapter 11

Electric field due to uniformly charged sphere class 12 physics JEE_Main

Physics Average Value and RMS Value JEE Main 2025

JEE Mains 2025 Correction Window Date (Out) – Check Procedure and Fees Here!




