
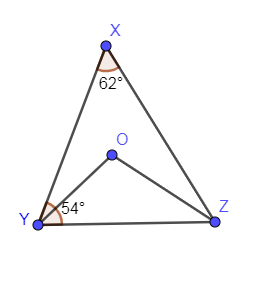
In the below figure, $\angle X={{62}^{\circ }}$, $\angle XYZ={{54}^{\circ }}$. If YO and ZO are the bisectors of angle Y and angle Z then find $\angle OZY\And \angle YOZ$.

Answer
579.6k+ views
Hint: We know that the sum of all the angles of a triangle are ${{180}^{\circ }}$ so using this property we can find the value of the third angle Z of the triangle XYZ because we know the values of angle X and angle Y. After that it is given that OY and OZ are the angle bisectors of angles Y and Z respectively so $\angle OYZ\And \angle OZY$ are half of angles Y and Z using this information we can find the value of $\angle OZY$ and $\angle YOZ$ is calculated by using the property of the triangle that sum of the all the angles of a triangle are ${{180}^{\circ }}$ and here the triangle is OYZ.
Complete step by step answer:
We have given a figure below, in which $\angle X={{62}^{\circ }}$, $\angle XYZ={{54}^{\circ }}$.
We are asked to find $\angle OZY\And \angle YOZ$.
First of all we are going to find the value of angle Z which we do by using the property of the triangle of XYZ that the sum of all angles of the triangle are ${{180}^{\circ }}$.
$\angle X+\angle Y+\angle Z={{180}^{\circ }}$
Substituting $\angle X={{62}^{\circ }}$ and $\angle Y={{54}^{\circ }}$ in the above equation we get,
$\begin{align}
& {{62}^{\circ }}+{{54}^{\circ }}+\angle Z={{180}^{\circ }}.......Eq.(1) \\
& \Rightarrow {{116}^{\circ }}+\angle Z={{180}^{\circ }} \\
& \Rightarrow \angle Z={{180}^{\circ }}-{{116}^{\circ }} \\
& \Rightarrow \angle Z={{64}^{\circ }} \\
\end{align}$
Hence, we got the value of angle Z as ${{64}^{\circ }}$.
It is also given that OY and OZ are the angle bisectors of angles Y and Z respectively. This means that the values of $\angle OYZ\And \angle OZY$ are equal to half of angle Y and half of angle Z respectively.
$\begin{align}
& \angle OYZ=\dfrac{1}{2}\angle Y \\
& \Rightarrow \angle OYZ=\dfrac{1}{2}\left( {{54}^{\circ }} \right) \\
& \Rightarrow \angle OYZ={{27}^{\circ }} \\
\end{align}$
From the above, we got the value of $\angle OYZ={{27}^{\circ }}$.
$\begin{align}
& \angle OZY=\dfrac{1}{2}\angle Z \\
& \Rightarrow \angle OZY=\dfrac{1}{2}\left( {{64}^{\circ }} \right) \\
& \Rightarrow \angle OZY={{32}^{\circ }} \\
\end{align}$
From the above, we got the value of $\angle OZY={{32}^{\circ }}$.
Now, to find the value of $\angle YOZ$ we are going to use the property of triangle which says that the sum of the angles of a triangle are ${{180}^{\circ }}$ in $\Delta YOZ$.
$\begin{align}
& \angle YOZ+\angle OZY+\angle OYZ={{180}^{\circ }} \\
& \Rightarrow \angle YOZ+{{32}^{\circ }}+{{27}^{\circ }}={{180}^{\circ }} \\
& \Rightarrow \angle YOZ+{{59}^{\circ }}={{180}^{\circ }} \\
& \Rightarrow \angle YOZ={{180}^{\circ }}-{{59}^{\circ }} \\
& \Rightarrow \angle YOZ={{121}^{\circ }} \\
\end{align}$
From the above, we got the value of $\angle YOZ={{121}^{\circ }}$.
Hence, we got the value of $\angle YOZ={{121}^{\circ }}$ and $\angle OZY={{32}^{\circ }}$.
Note: This question demands the knowledge of the property of a triangle which says that sum of all angles of the triangle are ${{180}^{\circ }}$ if you don’t know this property then you are lost in this problem and you cannot solve anything in it.
The mistake that could happen in this problem is the calculation mistakes so be careful. Another thing through which you can check whether the angles that you calculated are correct or not by using these angles in the equation of sum of all the angles of the triangle as ${{180}^{\circ }}$.
For e.g. to check whether $\angle OZY={{32}^{\circ }}$, first of all double it so that we will get the angle Z.
$2\angle OZY={{64}^{\circ }}=\angle Z$
Now, substituting the above value of angle Z in eq. (1) we get,
$\begin{align}
& {{62}^{\circ }}+{{54}^{\circ }}+{{64}^{\circ }}={{180}^{\circ }} \\
& \Rightarrow {{180}^{\circ }}={{180}^{\circ }} \\
\end{align}$
As you can see that L.H.S is equal to R.H.S so the value of $\angle OZY={{32}^{\circ }}$ which we have calculated is correct.
Complete step by step answer:
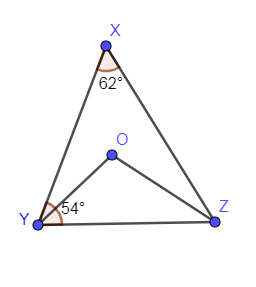
We have given a figure below, in which $\angle X={{62}^{\circ }}$, $\angle XYZ={{54}^{\circ }}$.

We are asked to find $\angle OZY\And \angle YOZ$.
First of all we are going to find the value of angle Z which we do by using the property of the triangle of XYZ that the sum of all angles of the triangle are ${{180}^{\circ }}$.
$\angle X+\angle Y+\angle Z={{180}^{\circ }}$
Substituting $\angle X={{62}^{\circ }}$ and $\angle Y={{54}^{\circ }}$ in the above equation we get,
$\begin{align}
& {{62}^{\circ }}+{{54}^{\circ }}+\angle Z={{180}^{\circ }}.......Eq.(1) \\
& \Rightarrow {{116}^{\circ }}+\angle Z={{180}^{\circ }} \\
& \Rightarrow \angle Z={{180}^{\circ }}-{{116}^{\circ }} \\
& \Rightarrow \angle Z={{64}^{\circ }} \\
\end{align}$
Hence, we got the value of angle Z as ${{64}^{\circ }}$.
It is also given that OY and OZ are the angle bisectors of angles Y and Z respectively. This means that the values of $\angle OYZ\And \angle OZY$ are equal to half of angle Y and half of angle Z respectively.
$\begin{align}
& \angle OYZ=\dfrac{1}{2}\angle Y \\
& \Rightarrow \angle OYZ=\dfrac{1}{2}\left( {{54}^{\circ }} \right) \\
& \Rightarrow \angle OYZ={{27}^{\circ }} \\
\end{align}$
From the above, we got the value of $\angle OYZ={{27}^{\circ }}$.
$\begin{align}
& \angle OZY=\dfrac{1}{2}\angle Z \\
& \Rightarrow \angle OZY=\dfrac{1}{2}\left( {{64}^{\circ }} \right) \\
& \Rightarrow \angle OZY={{32}^{\circ }} \\
\end{align}$
From the above, we got the value of $\angle OZY={{32}^{\circ }}$.
Now, to find the value of $\angle YOZ$ we are going to use the property of triangle which says that the sum of the angles of a triangle are ${{180}^{\circ }}$ in $\Delta YOZ$.
$\begin{align}
& \angle YOZ+\angle OZY+\angle OYZ={{180}^{\circ }} \\
& \Rightarrow \angle YOZ+{{32}^{\circ }}+{{27}^{\circ }}={{180}^{\circ }} \\
& \Rightarrow \angle YOZ+{{59}^{\circ }}={{180}^{\circ }} \\
& \Rightarrow \angle YOZ={{180}^{\circ }}-{{59}^{\circ }} \\
& \Rightarrow \angle YOZ={{121}^{\circ }} \\
\end{align}$
From the above, we got the value of $\angle YOZ={{121}^{\circ }}$.
Hence, we got the value of $\angle YOZ={{121}^{\circ }}$ and $\angle OZY={{32}^{\circ }}$.
Note: This question demands the knowledge of the property of a triangle which says that sum of all angles of the triangle are ${{180}^{\circ }}$ if you don’t know this property then you are lost in this problem and you cannot solve anything in it.
The mistake that could happen in this problem is the calculation mistakes so be careful. Another thing through which you can check whether the angles that you calculated are correct or not by using these angles in the equation of sum of all the angles of the triangle as ${{180}^{\circ }}$.
For e.g. to check whether $\angle OZY={{32}^{\circ }}$, first of all double it so that we will get the angle Z.
$2\angle OZY={{64}^{\circ }}=\angle Z$
Now, substituting the above value of angle Z in eq. (1) we get,
$\begin{align}
& {{62}^{\circ }}+{{54}^{\circ }}+{{64}^{\circ }}={{180}^{\circ }} \\
& \Rightarrow {{180}^{\circ }}={{180}^{\circ }} \\
\end{align}$
As you can see that L.H.S is equal to R.H.S so the value of $\angle OZY={{32}^{\circ }}$ which we have calculated is correct.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who among the following opened first school for girls class 9 social science CBSE

What does the word meridian mean A New day B Midday class 9 social science CBSE

What is the full form of pH?

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it





