Question

In the cube below, $AB=4$ . What is the perimeter of rectangle ABCD?

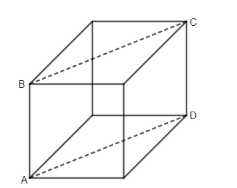
(a). 24
(b). \[16\sqrt{2}\] (approximately 22.63)
(c). \[16+4\sqrt{2}\] (approximately 21.66)
(d). \[8+8\sqrt{2}\] (approximately 19.31)
(e). \[4+8\sqrt{2}\] (approximately 15.31)

Answer 1

Hint: Firstly, we are asked to find the perimeter of rectangle ABCD. So, we are having one side and we have to find diagonal length BC or CD as it can be seen in the diagram. So, formula of perimeter of rectangle ABCD \[=2\left( AB+BC \right)\] which is same as \[=2\left( length+breadth \right)\] and to find diagonal of BC \[=\sqrt{2}AB\] .

Complete step-by-step answer:

Here, we are provided with one side of a cube $AB=4$ . We have to find perimeter of rectangle which means addition of 4 sides i.e. AB, BC, CD, AD. As it is cube, all the sides are of equal length except the diagonal BC and AD as shown in figure.

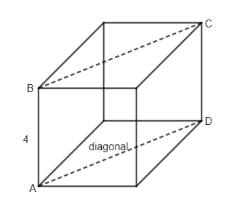
So, formula to find diagonal is given by:
Diagonal \[=\sqrt{2}\left( side \right)\]
\[=\sqrt{2}AB\]
\[=4\sqrt{2}\]
So, we have length of diagonal as \[AD=BC=4\sqrt{2}\]
Now, the formula to find the perimeter of the rectangle ABCD is \[=2\left( AB+BC \right)\] which we can consider AB as length and BC is breadth.
\[=2\left( 4+4\sqrt{2} \right)\]
\[=8+8\sqrt{2}\]
Thus, the perimeter of rectangle ABCD is \[8+8\sqrt{2}\] .
Option (d) is the correct answer.

Note: Another way for finding the perimeter of rectangle ABCD is adding all the values of 4 sides i.e. \[AB+BC+CD+AD\] which on substituting values gives the same answer. Generally, there are chances where students seeing the question of the cube take all the sides equal including the diagonals. So, the perimeter of the rectangle will be \[4+4+4+4=16\] which is the wrong answer. So, don’t make these silly mistakes.