Question

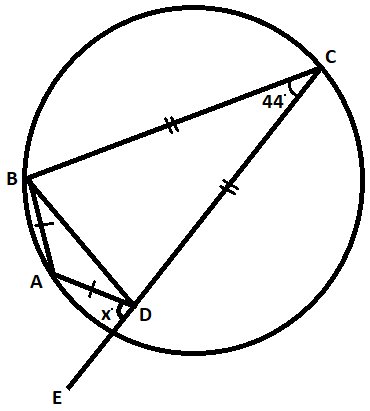
In the figure given below, $CDE$ is straight line and $A,B,C$ and $D$ are points on a circle. $\angle BCD = {44^ \circ }$, find the value of $x.$

Answer 1

Hint: To solve the above problem we have to know a few properties of a quadrilateral inscribed inside a circle. There are a few properties such as the sum of the opposite angles of a quadrilateral in a circle is ${180^ \circ }$, as long as the quadrilateral does not cross itself out of the circle. Here a four-sided polygon is inscribed in a circle.

Complete step by step answer:
Given that $\angle ADE = {x^ \circ }$
The opposite angles in a quadrilateral in a circle should be equal to ${180^ \circ }$, as long as the quadrilateral does not cross the circle.
$\therefore \angle BAD + \angle BCD = {180^ \circ }$
As given that $\angle BCD = {44^ \circ }$, substituting this in the above expression:
$ \Rightarrow \angle BAD + {44^ \circ } = {180^ \circ }$
\[ \Rightarrow \angle BAD = {180^ \circ } - {44^ \circ }\]
\[\therefore \angle BAD = {136^ \circ }\]
Now consider the triangle BCD, given that two sides are equal in this triangle, as given below:
$ \Rightarrow BC = CD$
Hence the angles opposite to these sides will also be equal, which is given below:
$ \Rightarrow \angle CBD = \angle CDB$
We know that the sum of the angles in a triangle should be equal to ${180^ \circ }$, as given below:
$ \Rightarrow \angle CBD + \angle BCD + \angle CDB = {180^ \circ }$
$ \Rightarrow \angle CBD + {44^ \circ } + \angle CDB = {180^ \circ }$
$ \Rightarrow 2\angle CDB = {180^ \circ } - {44^ \circ }$
\[ \Rightarrow 2\angle CDB = {136^ \circ }\]
\[\therefore \angle CDB = {68^ \circ }\]
Hence $\angle CBD = {68^ \circ }$
Now consider the triangle ABD, given that two sides are equal in this triangle, as given below:
$ \Rightarrow AB = AD$
Hence the angles opposite to these sides will also be equal, which is given below:
$ \Rightarrow \angle ABD = \angle ADB$
We know that the sum of the angles in a triangle should be equal to ${180^ \circ }$, as given below:
$ \Rightarrow \angle ABD + \angle BAD + \angle ADB = {180^ \circ }$
We found that \[\angle BAD = {136^ \circ }\], substituting this in the above expression, as shown below:
$ \Rightarrow {136^ \circ } + 2\angle ADB = {180^ \circ }$
$ \Rightarrow 2\angle ADB = {180^ \circ } - {136^ \circ }$
$ \Rightarrow 2\angle ADB = {44^ \circ }$
$ \Rightarrow \angle ADB = {22^ \circ }$
Hence $\angle ABD = {22^ \circ }$
Now we know that a straight angle forms an angle of ${180^ \circ }$, which is as given below:
Consider the straight line at the point D, which is given below:
$ \Rightarrow \angle CDB + \angle ADB + \angle ADE = {180^ \circ }$
\[ \Rightarrow {68^ \circ } + {22^ \circ } + \angle ADE = {180^ \circ }\]
\[ \Rightarrow \angle ADE = {180^ \circ } - {90^ \circ }\]
$ \Rightarrow \angle ADE = {90^ \circ }$
$\therefore x = {90^ \circ }$

The value of $x$ is ${90^ \circ }$.

Note: While solving such kinds of polygons inscribed inside a circle problems, one thing which is most important to remember is that the sum of the opposite angles of a quadrilateral which is in a circle is equal to ${180^ \circ }$. Also it is crucial to note that the sum of the angles in any quadrilateral is equal to ${360^ \circ }$.