
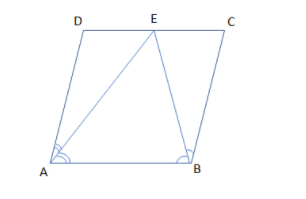
In the given figure ABCD is a parallelogram with AB=CD and AD=BC. Prove that AB=2BC.

Answer
575.4k+ views
Hint: First, before proceeding for this, we must know the following figure clearly depicts that some of the angles of this parallelogram ABCD are equal. Then, by applying the property of the parallelogram that AB||CD where AE is the transverse line which is cutting the sides AB and CD of the parallelogram which gives that the alternate opposite angles made across that line AE is equal. Then, we also know that if the two angles of a triangle which is triangle ADE are equal then the opposite sides to that angle are also equal and then after using the conditions in the question, we proved the desired result.
Complete step-by-step answer:
In this question, we are supposed to prove that AB=2BC where ABCD is a parallelogram with AB=CD and AD=BC as shown in the figure.
So, before proceeding for this, we must know the following figure clearly depicts that some of the angles of this parallelogram ABCD are equal as:
$\begin{align}
& \angle EAB=\angle EAD \\
& \angle EBA=\angle EBC \\
\end{align}$
Now, by applying the property of the parallelogram that AB||CD where AE is the transverse line which is cutting the sides AB and CD of the parallelogram which gives that the alternate opposite angles made across that line AE is equal as:
$\angle EAB=\angle AED$
Now, we already know that $\angle EAB=\angle EAD$from the given condition in the question which gives us:
$\angle EAD=\angle AED$
Now, we also know that if the two angles of a triangle which is triangle ADE are equal then the opposite sides to that angle are also equal.
So, from the above condition, we get:
AD=DE
Now, from the figure, we can clearly see that DE is the half of side DC, so we get the result as:
$AD=\dfrac{1}{2}DC$
Now, b y using the two conditions given in the question as AB=CD and AD=BC, we get:
$BC=\dfrac{1}{2}AB$
The, by rearranging the above equation, we get:
AB=2BC
Hence, we proved the desired result.
Note: Now, to solve these types of questions we need to know some of the basics of the parallel lines as when any line intersects two parallel lines then the angles made by that line are equal. Some of the angles which are equal are alternate opposite angles and vertically opposite angles.
Complete step-by-step answer:
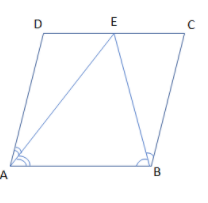
In this question, we are supposed to prove that AB=2BC where ABCD is a parallelogram with AB=CD and AD=BC as shown in the figure.

So, before proceeding for this, we must know the following figure clearly depicts that some of the angles of this parallelogram ABCD are equal as:
$\begin{align}
& \angle EAB=\angle EAD \\
& \angle EBA=\angle EBC \\
\end{align}$
Now, by applying the property of the parallelogram that AB||CD where AE is the transverse line which is cutting the sides AB and CD of the parallelogram which gives that the alternate opposite angles made across that line AE is equal as:
$\angle EAB=\angle AED$
Now, we already know that $\angle EAB=\angle EAD$from the given condition in the question which gives us:
$\angle EAD=\angle AED$
Now, we also know that if the two angles of a triangle which is triangle ADE are equal then the opposite sides to that angle are also equal.
So, from the above condition, we get:
AD=DE
Now, from the figure, we can clearly see that DE is the half of side DC, so we get the result as:
$AD=\dfrac{1}{2}DC$
Now, b y using the two conditions given in the question as AB=CD and AD=BC, we get:
$BC=\dfrac{1}{2}AB$
The, by rearranging the above equation, we get:
AB=2BC
Hence, we proved the desired result.
Note: Now, to solve these types of questions we need to know some of the basics of the parallel lines as when any line intersects two parallel lines then the angles made by that line are equal. Some of the angles which are equal are alternate opposite angles and vertically opposite angles.
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is pollution? How many types of pollution? Define it

What is the Full Form of ISI and RAW




