Question

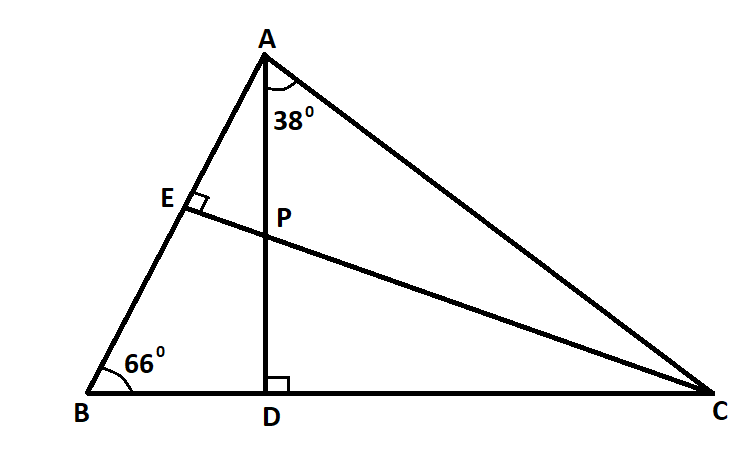
In the given figure, $\angle ABC = {66^0},\angle DAC = {38^0}$, CE is perpendicular to AB and AD is perpendicular to BC. Prove that CP > AP.

Answer 1

Hint: To answer this question, we will use some basic points of geometry of triangles. While solving this, we have to remember that the sides that are opposite to the greater angle will always be greater.

Complete step by step answer:
Given that,
$\angle ABC = {66^0}$ and $\angle DAC = {38^0}$
$CE \bot AB$ and $AD \bot BC$
We have to prove that,
CP > AP
Proof:
Consider quadrilateral BEPD,
We know that, the sum of all angles of a quadrilateral is ${360^0}$,
Therefore,
\[ \Rightarrow \angle BEP + \angle EPD + \angle PDB + \angle DBE = {360^0}\] …………. (i)
We have given, $\angle ABC = {66^0}$
We know that E and D are points on AB and BC.
Therefore, $\angle DBE = {66^0}$
We also know that if a line is perpendicular to another line, then the angle subtended at that point will be ${90^0}$.
Thus, $\angle BEP = \angle PDB = {90^0}$
Putting all these values in equation (i), we will get
\[
   \Rightarrow {90^0} + \angle EPD + {90^0} + {66^0} = {360^0} \\
   \Rightarrow \angle EPD + {246^0} = {360^0} \\
   \Rightarrow \angle EPD = {360^0} - {246^0} \\
   \Rightarrow \angle EPD = {114^0} \\
\]
We got, \[\angle EPD = {114^0}\]
Therefore,
\[\angle APC = {114^0}\] [ opposite angles are equal ]
Now, In $\vartriangle ABC$
$ \Rightarrow \angle APC + \angle PCA + \angle PAC = {180^0}$ ( sum of all angles of a triangle is ${180^0}$ )
D is a point on line BC, so
$\angle DAC = \angle PAC = {38^0}$.
Putting all these values, we will get
\[
   \Rightarrow {114^0} + \angle PCA + {38^0} = {180^0} \\
   \Rightarrow \angle PCA + {152^0} = {180^0} \\
   \Rightarrow \angle PCA = {180^0} - {152^0} \\
   \Rightarrow \angle PCA = {28^0} \\
\]
Here, we can see that \[\angle PCA = {28^0}\] and \[\angle PAC = {38^0}\].
\[\angle PAC > \angle PCA\] as \[{38^0} > {28^0}\].
Therefore, the side CP > AP because the side opposite to the greater angle is greater and CP is opposite to $\angle PAC$, which is greater.
Hence proved.

Note: Whenever we ask such types of questions, we will use some basic properties of triangles. First, we have to find out all the given details and what we have to prove. Then we will consider some portion of the figure and then by applying necessary properties, we will find out the angles of the figure. After that, we will get all the required angles and then by using the property that ‘side opposite to the greater angle is greater’, we will get the required answer.