Question

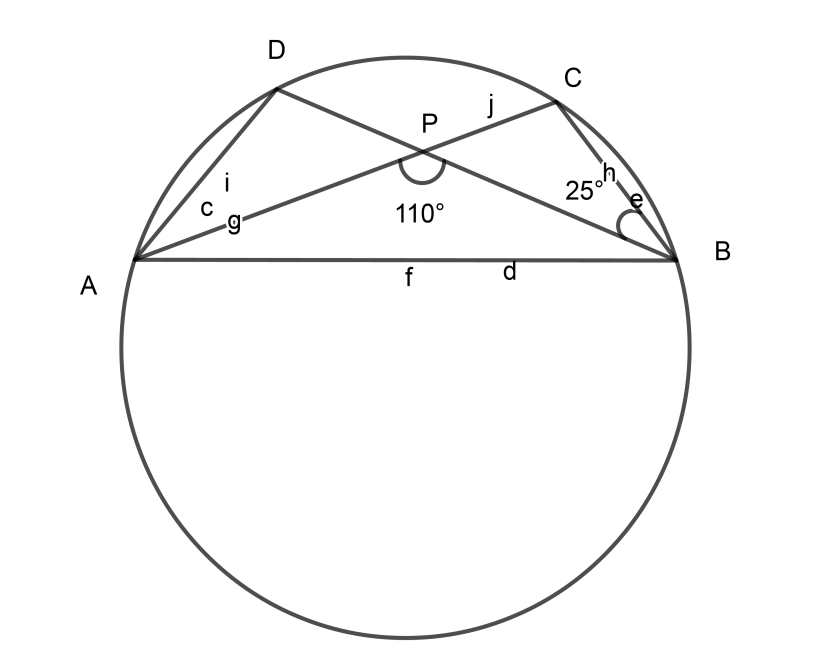
In the given figure, O is the centre of the circle. If $\angle PBC = 25^\circ and \angle APB = 110^\circ $, find the value of $\angle ADB$

Answer 1

Hint: We can solve this problem by using the concept i.e.
Angles inscribed by same arc on the circumference of circle are always EQUAL

Complete step-by-step answer:
We will write the given first,
$\angle PBC = 25^\circ and \angle APB = 110^\circ $……………………………. (1)
To find the a$\angle ADB$ we should know the key concept given below,
Concept: Angles inscribed by same arc on the circumference of circle are always EQUAL
Therefore we can say Angles inscribed by arc AB are equal. That is,
$\angle ADB = \angle ACB$…………………………………. (2)
Now let’s find$\angle ACB$,
As we all know $\angle APC$ is a straight angle,
$\angle APC = 180^\circ $
But, $\angle APC$can be written as,
$\angle APC = \angle APB + \angle CPB$
$\therefore 180^\circ = 110^\circ + \angle CPB$………………………….. [From (1)]
$\therefore \angle CPB = 180^\circ - 110^\circ $
$\therefore \angle CPB = 70^\circ $……………………………….. (3)

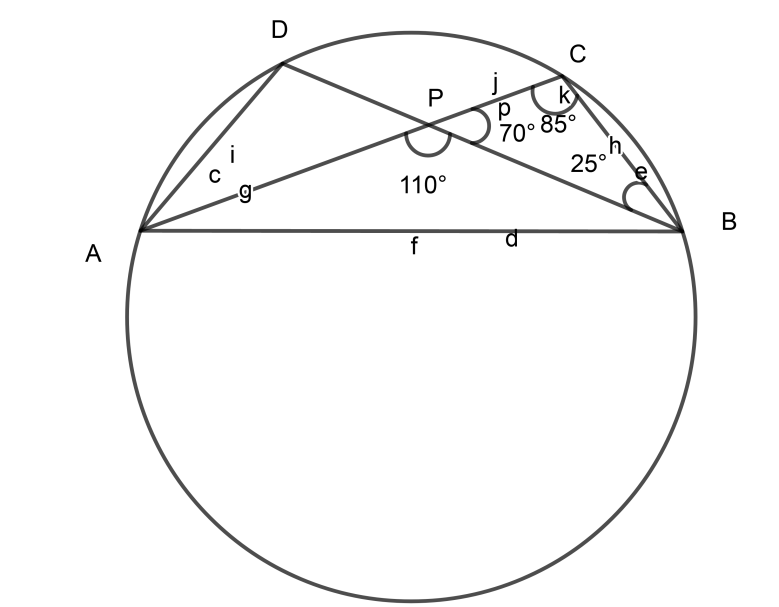
Now consider $\triangle BPC$,
As the property of a triangle says that the sum of three angles of a triangle are $180^\circ $,
$\angle CPB + \angle PBC + \angle BCP = 180^\circ $
$\therefore 70^\circ + 25^\circ + \angle BCP = 180^\circ $
$\therefore \angle BCP = 180^\circ - 95^\circ $
$\therefore \angle BCP = 85^\circ $
We can write $\angle BCP$ as $\angle PCB$
$\therefore \angle PCB = 85^\circ $
Now if we see the figure we will come to know that $\angle PCB = \angle ACB$ as P and A lie on the same line.
$\therefore \angle ACB = 85^\circ $
Our target is to find the ∠ADB therefore rewrite the equation (2)
$\therefore \angle ADB = \angle ACB$
Put the value of$\angle ACB = 85^\circ $,
$\therefore \angle ADB = 85^\circ $
Therefore the value of $\angle ADB$ is $85^\circ $.

Note: Always remember to draw diagrams for this type of problems to avoid confusion. Also, the property of a circle given by “Angles inscribed by the same arc on the circumference of a circle are always EQUAL” is very much important to solve this problem.