Question

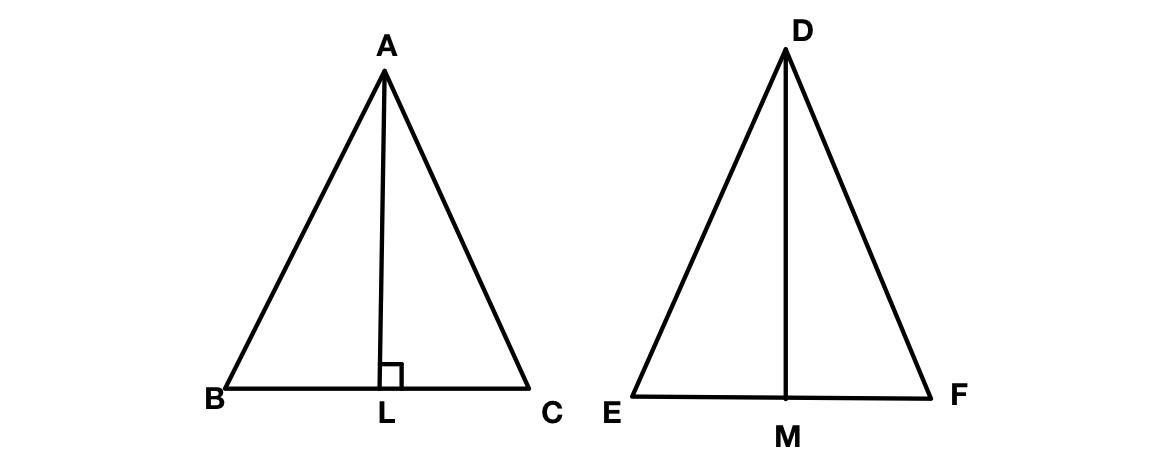
In the given figure two isosceles triangles have equal vertical angles and their areas are in the ratio 16:25. Find the ratio of their corresponding heights,

Answer 1

Hint: In this question it is given that two isosceles triangles $\triangle ABC$ & $\triangle DEF$ have equal vertical angles $\angle BAC=\angle EDF$ and their areas are in the ratio 16:25, i,e, $$\dfrac{area\left( \triangle ABC\right) }{area\left( \triangle DEF\right) } =\dfrac{16}{25}$$.
We have to find the ratio of their corresponding heights, i.e, AL:DM.
So to find the solution we need to know that, if two triangles are similar, then the ratio of their area is equal to the ratio of the squires of their corresponding sides.

Complete step-by-step solution:
Given, AB=AC and DE=DF
Which can be written as, $$\dfrac{AB}{AC} =1$$ & $$\dfrac{DE}{DF} =1$$
Therefore,
$$\dfrac{AB}{AC} =\dfrac{DE}{DF}$$
$$\Rightarrow \dfrac{AB}{DE} =\dfrac{AC}{DF}$$
Also, AL$\bot$BC and DM$\bot$EF.
Now since the vertical angles are equal, i.e $\angle BAC=\angle EDF$ and $$\dfrac{AB}{DE} =\dfrac{AC}{DF}$$.
Therefore, by SAS(Side-Angle-Side) similarity criterion we can say that $$\triangle ABC\sim \triangle DEF$$
So we can write,
$$\dfrac{area\left( \triangle ABC\right) }{area\left( \triangle DEF\right) } =\left( \dfrac{AB}{DE} \right)^{2} =\left( \dfrac{AL}{DM} \right)^{2} $$
$$\Rightarrow \dfrac{area\left( \triangle ABC\right) }{area\left( \triangle DEF\right) } =\left( \dfrac{AL}{DM} \right)^{2} $$
$$\Rightarrow \dfrac{16}{25} =\left( \dfrac{AL}{DM} \right)^{2} $$
$$\Rightarrow \left( \dfrac{AL}{DM} \right)^{2} =\dfrac{16}{25}$$
$$\Rightarrow \left( \dfrac{AL}{DM} \right) =\sqrt{\dfrac{16}{25} }$$
$$\Rightarrow \left( \dfrac{AL}{DM} \right) =\dfrac{4}{5}$$
$\therefore$ AL:DM = 4:5
So the ratio of their corresponding sides is 4:5.

Note: To solve this type of question you have to remember that when each corresponding side of two isosceles triangles is proportional to each other then their height (altitude) must be proportional to each other, in other way we can write that, for $\triangle ABC$ and $\triangle DEF$
If, $$\dfrac{AB}{DE} =\dfrac{BC}{EF} =\dfrac{AC}{DF}=k$$, where k is some constant,
Then,$$\dfrac{AL}{DM} =k$$.
i.e, $$\dfrac{AB}{DE} =\dfrac{BC}{EF} =\dfrac{AC}{DF}=\dfrac{AL}{DM}$$.