Question

In the given figure what is the ratio of ammeter reading when J is connected to A and then to B.

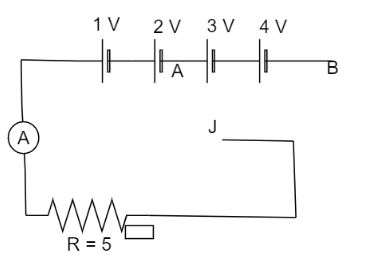
Answer 1

Hint:Here we will complete the circuit by using jockey, J. Firstly we will connect J to point A thus it will eliminate the \[3{\text{ V}}\] and \[{\text{4 V}}\] cell out of the circuit. Thus we will find the current flowing through the circuit. Similarly we will connect J to point B then all the cells involved in the circuit. Thus we can find the ration in both the situations.

Complete step by step answer:
\[(1).\] When the Jockey, J is connected to point A then the figure will look like:

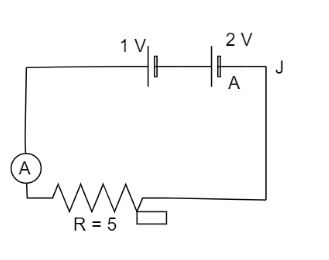
Thus total voltage is equal to \[\left( {1 + 2} \right){\text{ = 3 V}}\]. Since there is no internal resistance in the circuit. Therefore the amount of current \[\left( {{I_A}} \right)\] flowing when J is connected to A is equal to:
\[{{\text{I}}_A}{\text{ = }}\dfrac{{\text{V}}}{R}\]
\[\Rightarrow {{\text{I}}_A}{\text{ = }}\dfrac{3}{5}{\text{ A}}\] _____________\[(i)\]

\[(2).\] When Jockey, J is connected to point B then the figure will look like as below:

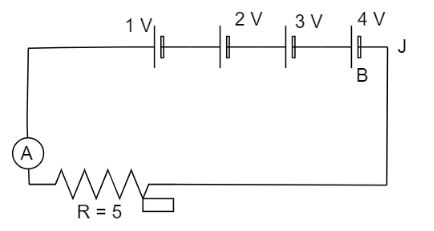
Here all the cells involved in the circuit. Therefore the total voltage in the circuit will be equal to sum of all the voltages as:
\[V{\text{ = 1 V + 2 V + 3 V + 4 V}}\]
\[\Rightarrow V{\text{ = 10 V}}\]
The current \[\left( {{I_B}} \right)\] flowing through the circuit when J is connected to point B is equal to:
\[{{\text{I}}_B}{\text{ = }}\dfrac{{\text{V}}}{R}\]
\[\Rightarrow {{\text{I}}_B}{\text{ = }}\dfrac{{{\text{10 V}}}}{5}\]
\[\Rightarrow {{\text{I}}_B}{\text{ = 2 A}}\] ____________\[(ii)\]
Thus we get the value of current in both the cases. Now dividing equation \[(i)\] and equation \[(ii)\] we get the ratio of current in both cases as:
\[\dfrac{{{{\text{I}}_A}}}{{{{\text{I}}_B}}}{\text{ = }}\dfrac{{\dfrac{3}{5}{\text{ A}}}}{{2{\text{ A}}}}\]
\[\therefore \dfrac{{{{\text{I}}_A}}}{{{{\text{I}}_B}}}{\text{ = }}\dfrac{{\text{3}}}{{10}}\]

Thus the ratio of current is \[3:10\].

Note:It must be noted while calculating the total voltage in the circuit the polarity of the cell must be taken care of. If a negative terminal of a cell is connected to the positive of another cell then potential difference gets subtracted. Also if there is some internal resistance then total resistance will be the sum of its internal resistance and given external resistance.