Question

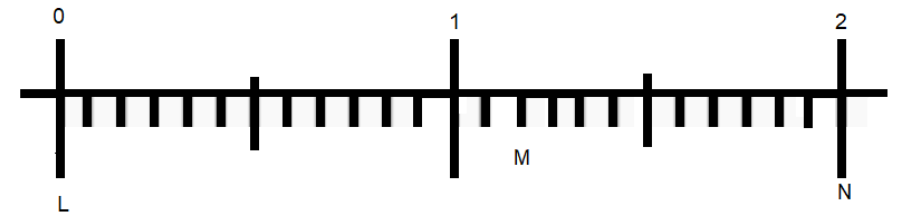
In the given number line, point M represents a fractional number. Find the number.

Answer 1

Hint: We first need to find the difference between normal scaling and the one we have been provided with. Then we try to figure out the number of dividers and the distances between any two bigger units of 1 unit. We find out the distance of smaller scales. Then we add the distance of mark M from 1 to find the fractional number.

Complete step by step answer:
We have 3 given numbers 0, 1, 2 on the scale which is different than usual scales.
In usual ones we have 10 divisions of spaces with the help of 9 dividing lines between any two bigger numbers of 1 unit. All the small spaces equal to 0.1-unit length.
But in the given scaling system we have 11 dividers between two bigger numbers of 1 unit which has created 12 small spaces. The total distance between two numbers is still 1 unit.
So, a total 12 small spaces are adding up to create the distance of 1 unit. Using a unitary system, we can tell that 1 small space is going to be the distance of $\dfrac{1}{12}$ unit.
Now we need to find the fractional number of the point M.
This point is on the 2 steps to the right side of the mark 1.
Between the mark 1 and point M, there are 2 spaces which have a total distance of $2\times \dfrac{1}{12}=\dfrac{1}{6}$ unit.
So, the mark of M is the value of $1+\dfrac{1}{6}=\dfrac{7}{6}$ unit.
The mark M represents the fractional number $\dfrac{7}{6}$.

Note: We have to be careful about the number of dividers and number of spaces. Easiest way to remember is that the number of spaces will always be 1 greater than the number of dividers iff the end points are bounded. The spacing in between decides the fractional number value rather than the dividers.