Question

In triangle ABC DE||BC. Prove that the triangles ADC and AEB have equal area.

Answer 1

Hint: Use the fact that the triangles on the same base and between the same parallels are equal in area to prove that the area of the triangles DBC and EBC are equal. Subtract the area of the triangle OBC on both sides and add the areas of the triangles ODE and ADE on both sides to prove that the triangles ADC and AEB are equal in area.

Complete step-by-step answer:

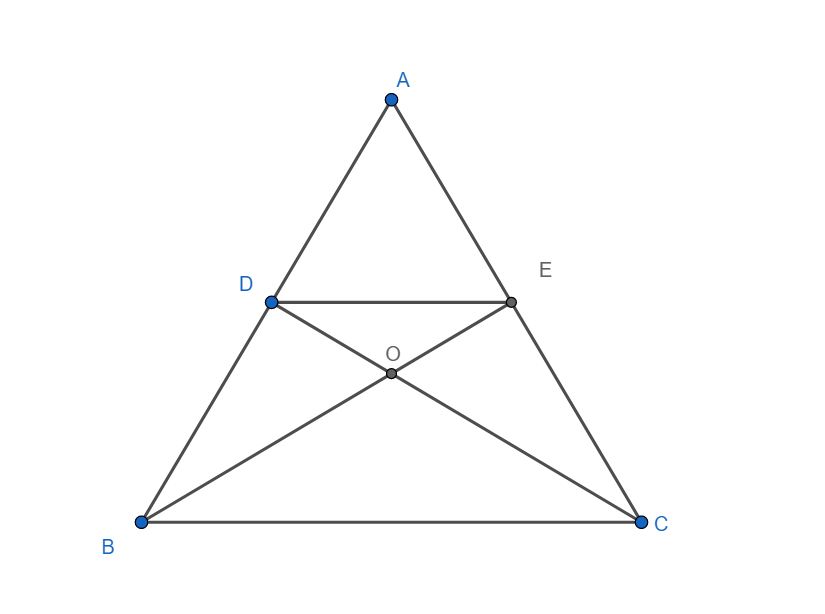
Given: A triangle ABC. Point D on AB and E on AC are such that DE||BC
To prove: Triangles ADC and AEB are equal in area.

Proof:
Triangle DBC and EBC are triangles on the same base BC and between the same parallels BC and DE. We know that the triangle on the same base and between the same parallels are equal in area. Hence, we have $ar\left( \Delta DBC \right)=ar\left( \Delta EBC \right)$
Subtracting $ar\left( \Delta BOC \right)$ on both sides, we get
$ar\left( \Delta DBC \right)-ar\left( \Delta BOC \right)=ar\left( \Delta EBC \right)-ar\left( \Delta BOC \right)$
From the diagram, it is clear that $ar\left( \Delta DBC \right)-ar\left( \Delta BOC \right)=ar\left( \Delta DOB \right)$
Similarly, we have $ar\left( \Delta EBC \right)-ar\left( \Delta BOC \right)=ar\left( \Delta EOC \right)$
Hence, we have
$ar\left( \Delta DOB \right)=ar\left( \Delta EOC \right)$
Adding $ar\left( \Delta DOE \right)$ on both sides, we get
$ar\left( \Delta DOB \right)+ar\left( \Delta DOE \right)=ar\left( \Delta EOC \right)+ar\left( \Delta DOE \right)$
From the diagram, it is clear that $ar\left( \Delta DOB \right)+ar\left( \Delta DOE \right)=ar\left( \Delta DEB \right)$
Similarly, we have $ar\left( \Delta EOC \right)+ar\left( \Delta DOE \right)=ar\left( \Delta DEC \right)$
Hence, we have $ar\left( \Delta DEB \right)=ar\left( \Delta DEC \right)$
Adding $ar\left( \Delta ADE \right)$ on both sides, we get
\[ar\left( \Delta DEB \right)+ar\left( \Delta ADE \right)=ar\left( \Delta DEC \right)+ar\left( \Delta ADE \right)\]
From the diagram, it is clear that $\left( \Delta DEB \right)+ar\left( \Delta ADE \right)=ar\left( \Delta AEB \right)$
Similarly, we have $ar\left( \Delta DEC \right)+ar\left( \Delta ADE \right)=ar\left( \Delta ADC \right)$
Hence, we have $ar\left( \Delta AEB \right)=ar\left( \Delta ADC \right)$
Hence proved.

Note: [1] In the above question, we have used the property that the areas of the triangles on the same base and between the same parallels are equal. This can be proved as follows

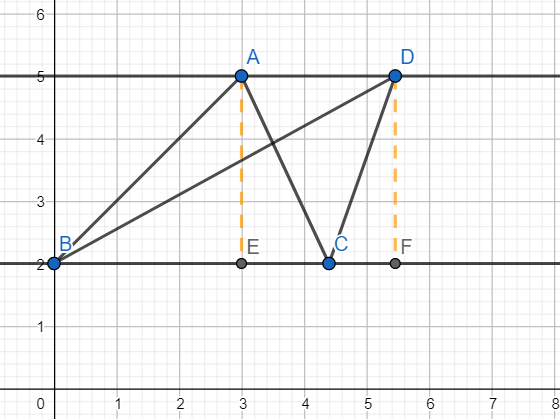
Consider the triangles ABC and DBC which are on the same base BC and between the same parallels AD and BC.
Draw perpendiculars AE and DF as shown.
We have AE = DF(Because AD||EF)
Hence area of triangle ABC $=\dfrac{1}{2}BC\times AE$ and area of the triangle DBC $=\dfrac{1}{2}DF\times BC=\dfrac{1}{2}AE\times BC$
Hence the triangles ABC and DBC are equal in area.
Hence the area of the triangles on the same base and between the same parallels are equal.