Question

In triangle $\Delta DEF$,\[\angle D={{87}^{\circ }}\] and \[\angle F={{43}^{\circ }}\]. If \[\Delta DEF\cong \Delta BAC\], then find the measure of \[\angle A\].

Answer 1

Hint: In this question we have been given with two triangles which are $\Delta DEF$ and $\Delta BAC$, we have given with the measure of two angles from triangle $\Delta DEF$ which are \[\angle D={{87}^{\circ }}\] and \[\angle F={{43}^{\circ }}\]. Now since we have been given with two angles in the given triangle, we will use the property of triangle which states that the sum of all the angles in a triangle is ${{180}^{\circ }}$. Using this property, we will find the value of \[\angle E\]. And since we have been given that the two triangles are congruent, we will use the property of congruent triangles to get the value of \[\angle A\] and get the required solution.

Complete step by step solution:
We know that in $\Delta DEF$,\[\angle D={{87}^{\circ }}\] and \[\angle F={{43}^{\circ }}\].
Now we know that the sum of all the angles in a triangle is equal to ${{180}^{\circ }}$.
This means that the sum of \[\angle D\],\[\angle E\] and \[\angle F\] will be ${{180}^{\circ }}$.
Mathematically, we can write it as:
$\Rightarrow \angle D+\angle E+\angle F={{180}^{\circ }}$
On substituting the values of \[\angle D={{87}^{\circ }}\] and \[\angle F={{43}^{\circ }}\], we get:
$\Rightarrow {{87}^{\circ }}+\angle E+{{43}^{\circ }}={{180}^{\circ }}$
On adding the angles in the left-hand side, we get:
$\Rightarrow \angle E+{{130}^{\circ }}={{180}^{\circ }}$
On transferring the term ${{130}^{\circ }}$ from the left-hand side to the right-hand side, we get:
$\Rightarrow \angle E={{180}^{\circ }}-{{130}^{\circ }}$
On simplifying, we get:
$\Rightarrow \angle E={{50}^{\circ }}$
Therefore, we have $\Delta DEF$ as follows:

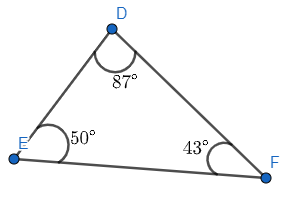
Now we know that triangles \[\Delta DEF\cong \Delta BAC\], now since both the triangles are congruent, the corresponding angles of the triangle are equal. Therefore, we can create triangle \[\Delta BAC\] with the same angles as follows:

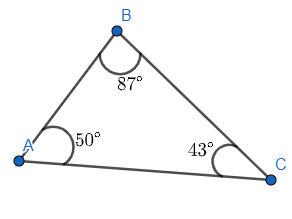
Now from the diagram, we can see that \[\angle A={{50}^{\circ }}\], which is the required solution.

Note: It is to be noted that the length of the sides of the two triangles also have the same lengths because congruency in triangles implies that all the corresponding sides and the angles of the triangle are equal. Since we have congruence as \[\Delta DEF\cong \Delta BAC\], we have \[\angle E=\angle A\] since they are both the middle angles.