Question

What is the inner surface area of a spherical shell of inner radius 15 cm and outer radius 16 cm? (correct up to 2 decimal places)
A). \[706.86\,c{{m}^{2}}\]
B). \[804.25\,c{{m}^{2}}\]
C). \[2827.43\,c{{m}^{2}}\]
D). \[3216.99\,c{{m}^{2}}\]

Answer 1

Hint: To solve this type of question, first of all we need to draw figure for understanding the question then we know that the inner radius \[r\] of sphere equals its surface area \[4\pi \,{{r}^{2}}\]. By substituting the value of inner radius in the given formula and by further solving this we get the value of inner surface area.

Complete step-by-step solution:
In this question it is given a spherical shell where inner and outer radius are given.
Here the spherical shell of inner radius 15 cm and outer radius 16 cm is given.
We can draw the diagram:

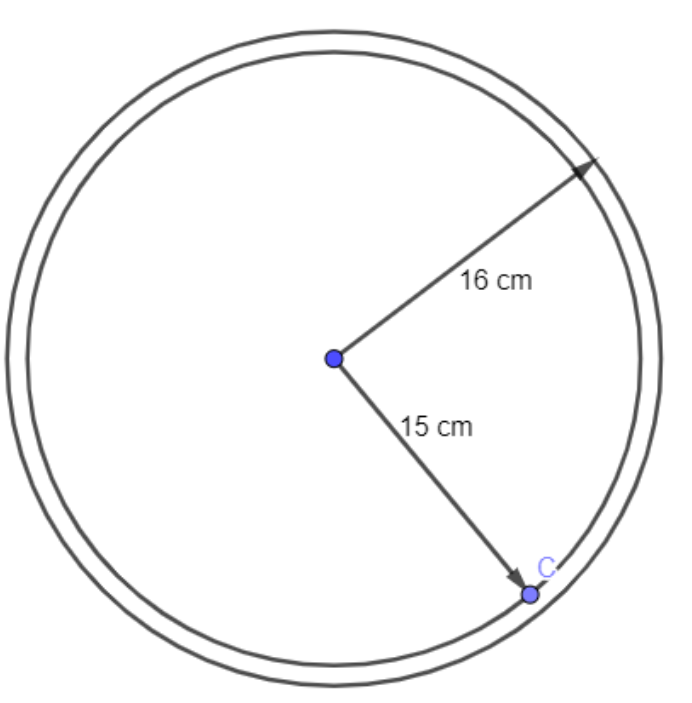
This is the 2D image but let us assume it in 3D vision. There is a sphere of radius 16 cm and another sphere of radius 15 cm which is inside that sphere.
So, according to the question, you are asked to find out the outer surface area of the spherical shell.
Now, we know that the inner surface area of the sphere is equal to\[4\pi \,{{r}^{2}}\]and substitute the value of inner radius in this formula. In this particular problem, we don’t use outer radius because we have asked about inner surface area. That means to calculate that we need to use an inner radius that is 15 cm. Not use an outer radius that is 16 cm.
So, the inner surface area can be given by \[4\pi \,{{r}^{2}}\]where \[\,r\] is the radius of the inner spherical shell that is 15 cm.
So, inner surface area\[=4\pi \,{{r}^{2}}\]
Putting \[\pi =\dfrac{22}{7}\,\]value, we will get:
Inner surface area\[=4\times \dfrac{22}{7}\times \,15\,\times 15\]
By simplifying this we get:
Inner surface area\[=2827.43388\,c{{m}^{2}}\]
So, correcting up to 2 decimals places we get:
Inner surface area\[=2827.43\,c{{m}^{2}}\]
So, the correct option is “option C”.

Note: We should not confuse the surface area of the circle and the surface area of the sphere as the circle is a 2D figure and its area is \[\pi \,{{r}^{2}}\]. But the sphere is a \[4\pi \,{{r}^{2}}\]. Sometimes students make mistakes by substituting the value of outer radius that is 16 cm. That is wrong because you are not asked to find the outer surface area. So, students should solve these types of problems.