Question

When the length of each side of a cube is increased by 3 cm, its volume is increased by $2457\,c{{m}^{3}}$ . Find its side. How much will its volume decrease, if the length of each side is reduced by 20%?
A.$16\,cm,\,1647\,c{{m}^{3}}$
B.$15\,cm,\,1647\,c{{m}^{3}}$
C.$17\,cm,\,1647\,c{{m}^{3}}$
D.$11\,cm,\,1647\,c{{m}^{3}}$

Answer 1

Hint: The given problem is related to absolute change. Consider the length of each side as x cm. Calculate its volume in terms of x. On increasing the length by 3 cm, it becomes (x+3) cm. Calculate the volume in terms of x. The difference in volume is given as $2457\,c{{m}^{3}}$. Find the value of x using this information. Then, find the reduced side and corresponding volume. Find the value of the decrease in volume.

Complete Step-by-step answer:
We will consider the length of the side of the cube as x cm. We know, the volume of a cube of side a cm is given as ${{a}^{3}}\,c{{m}^{3}}$ . So, the volume of the cube with side x cm is equal to ${{x}^{3}}\,c{{m}^{3}}$.
 This cube can be visualized as shown:

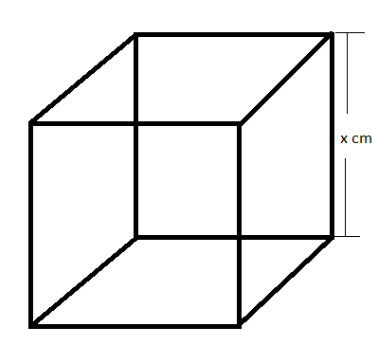
Now, it is given that the length of each side is increased by 3 cm. So, the new length of each side of the cube becomes (x + 3) cm. So, the new volume of the cube is ${{\left( x+3 \right)}^{3}}\,c{{m}^{3}}$ .
This cube can be visualized as shown:

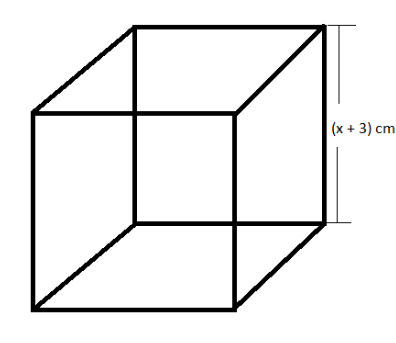
 Now, we know, the expansion of ${{\left( a+b \right)}^{3}}$ is given as ${{\left( a+b \right)}^{3}}={{a}^{3}}+{{b}^{3}}+3ab\left( a+b \right)$ . So, the value of ${{\left( x+3 \right)}^{3}}$ is equal to ${{x}^{3}}+27+9x\left( x+3 \right)$ . So, the new volume of the cube is \[\left( {{x}^{3}}+27+9x\left( x+3 \right) \right)c{{m}^{3}}\] . Now, in the question, it is given that the new volume is greater than the old volume by $2457\,c{{m}^{3}}$ . So, \[\left( {{x}^{3}}+27+9x\left( x+3 \right) \right)-{{x}^{3}}=2457\].
$\Rightarrow 9{{x}^{2}}+27x+27=2457$
$\Rightarrow {{x}^{2}}+3x+3=273$
$\Rightarrow {{x}^{2}}+3x-270=0$
The above equation is quadratic in x. We can solve it by splitting the middle term. We have to split 3x into two terms such that their sum is equal to 3x and their product is equal to $-270{{x}^{2}}$ . We can write 3x as (18x – 15x). So, the equation becomes \[{{x}^{2}}+18x-15x-270=0\] .
$\Rightarrow x\left( x+18 \right)-15\left( x+18 \right)=0$
$\Rightarrow \left( x-15 \right)\left( x+18 \right)=0$
So, either x = 15 or x = -18. We know, x is the length of the side of the cube. So, it cannot be negative. So, x = 15 cm. So, the original volume of the cube is equal to ${{\left( 15 \right)}^{3}}\,c{{m}^{3}}=3375\,c{{m}^{3}}$ .
Now, on decreasing the length of the side by 20%, the resulting side becomes (15 – 20% of 15) cm. So, the resulting side is equal to 15 – 3 = 12 cm. So, the resultant volume becomes ${{12}^{3}}\,c{{m}^{3}}=1728\,c{{m}^{3}}$ . Hence, the change in volume is equal to $3375-1728=1647\,c{{m}^{3}}$ .
Hence, option B. is the correct option.

Note: Be careful while doing calculations. The problem contains the use of identities which should be remembered properly, as getting them wrong can lead to wrong answers. Also, the absolute change in the value of an entity is calculated as (final value – initial value) and not (initial value – final value).