Question

Let ABCD be a tetrahedron such that the edges AB, AC, and AD are mutually perpendicular. Let the area of triangles ABC, ACD and ADB be 3,4 and 5sq.units, respectively, then the area of triangle BCD is
A. $5\sqrt 2 $
B. $5$
C. $\dfrac{{\sqrt 5 }}{2}$
D. $\dfrac{5}{2}$

Answer 1

Hint: Here in this question first we have to draw a diagram for better understanding of the question. We have an area of three triangles given in the question. Find the length of the side of the triangle with the help of the area of triangle formula.

Complete step-by-step answer:
First draw the diagram we have given in the question that
Area of triangle ABC = 3 Square unit
Area of triangle ACD = 4 square unit
Area of triangle ADB = 5 square unit

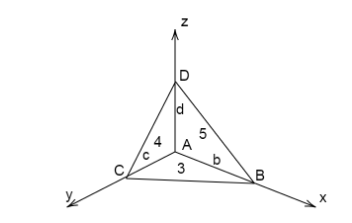
With the help of the diagram we can find the coordinates of the points
Coordinates of point C = $(c,0,0)$
Coordinates of point B =$(0,b,0)$
Coordinates of point D = $(0,0,d)$
Area of the triangle = $\dfrac{1}{2}.base.height$
So, the area of triangle ABC = $\dfrac{1}{2}cb$
$3 = \dfrac{1}{2}bc$
$bc = 6sq.unit$
Area of the triangle ACD = $ = \dfrac{1}{2}dc$
$4 = \dfrac{1}{2}cd$
$cd = 8sq.unit$
Area of the triangle = $ = \dfrac{1}{2}bd$
$5 = \dfrac{1}{2}bd$
$bd = 10sq.unit$
We can find the area of triangle of three coordinates by using vector method
Area of triangle BCD = $\dfrac{1}{2}\left| {\overrightarrow {BC} .\left. {\overrightarrow {BD} } \right|} \right.$
vector can be solved by subtracting coordinates of one point from second point
Here $\overrightarrow {BC} = < 0,c,0 > - < b,0,0 > $
$ = < 0 - b,c - 0,0 - 0 > $
subtracting the coordinates
$ = < - b,c,0 > $
$\overrightarrow {BD} = < b,0,0 > - < 0,0,d > $
$ = < b - 0,0 - 0,0 - d > $
$ = < b,0, - d > $
Use the detriments method for solving the vector
\[\overrightarrow {BC} .\overrightarrow {BD} = \left. {\left| {\begin{array}{*{20}{c}}
  i&j&k \\
  { - b}&c&0 \\
  { - b}&0&d
\end{array}} \right.} \right|\]
now solve the matrix
$ = i(cd) - j( - bd) + k(bc)$
open the brackets
$ = cdi + bdj + bck$
Squaring the components, we get
$\left| {\left. {\overrightarrow {BC} .\overrightarrow {BD} } \right|} \right. = \sqrt {{{(cd)}^2} + {{(bd)}^2} + {{(bc)}^2}} $
Area of the triangle BDC =
= $\dfrac{1}{2}.$$\sqrt {{{(cd)}^2} + {{(bd)}^2} + {{(bc)}^2}} $
Put the values
= $\dfrac{1}{2}\sqrt {{8^2} + {{10}^2} + {6^2}} $
Solve the square of number
= $\dfrac{1}{2}.\sqrt {64 + 100 + 36} $
Add the numbers
= $\dfrac{1}{2}\sqrt {200} $
= $\dfrac{{10\sqrt 2 }}{2}$
$ = 5\sqrt 2 sq.unit$

Hence, option A is the correct option.

Note: Find the area of the triangle using determinants method. Students mostly make mistakes in the part where we have to find the coordinates of points. Use the vector method. The sum of angles in a tetragon is $360^\circ$.