
Let ‘s’ denote the semiperimeter of a triangle ABC in which
Answer
451.8k+ views
Hint: We know that the semi perimeter of a triangle is given by
Complete step by step solution:
Let’s draw the diagram for the given data.
Also the circle touches the sides BC, CA, AB at D, E, F respectively.
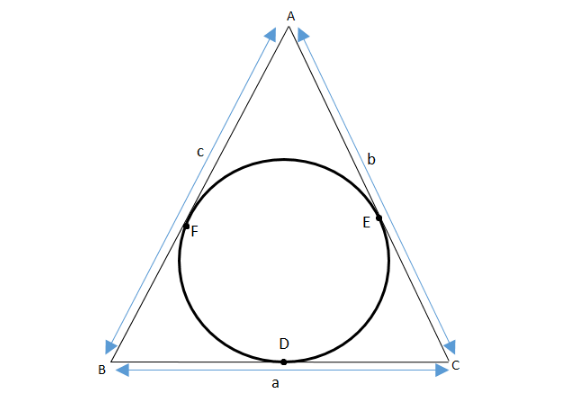
So the semi-perimeter is given according to the question is
B is an external point and BD and BF are tangents and from an external point the tangents drawn to a circle are equal in length.
That is,
(The length of tangents drawn from an external point to a circle are equal.)
Similarly we have,
Also given ‘s’ is semi perimeter
From the diagram we have,
Substituting these in equation (1) we have,
Now using equation (1), (2) and (3) we have,
But
But we know that
Rearranging we have,
Hence proved.
Note: We know that if we want perimeter we add all the side lengths of a given dimension. We know that the perimeter of a triangle is
Complete step by step solution:
Let’s draw the diagram for the given data.
Also the circle touches the sides BC, CA, AB at D, E, F respectively.

So the semi-perimeter is given according to the question is
B is an external point and BD and BF are tangents and from an external point the tangents drawn to a circle are equal in length.
That is,
(The length of tangents drawn from an external point to a circle are equal.)
Similarly we have,
Also given ‘s’ is semi perimeter
From the diagram we have,
Substituting these in equation (1) we have,
Now using equation (1), (2) and (3) we have,
But
But we know that
Rearranging we have,
Hence proved.
Note: We know that if we want perimeter we add all the side lengths of a given dimension. We know that the perimeter of a triangle is
Latest Vedantu courses for you
Grade 6 | CBSE | SCHOOL | English
Vedantu 6 Pro Course (2025-26)
School Full course for CBSE students
₹45,300 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What is pollution? How many types of pollution? Define it




