
Locate
Answer
521.7k+ views
Hint: In this question we will use the methods of representing a number on number line. Every real number is represented by a unique point on the number line. Also every point on the number line represents a unique real number. We will locate a number on the number line by using Pythagoras theorem.
Complete step-by-step solution:
Here , we have to locate
We will do this by using the Pythagoras theorem.
Here, we can write
We know that , according to Pythagoras theorem ,
By comparing this with equation (i) ,we get
Hypotenuse =
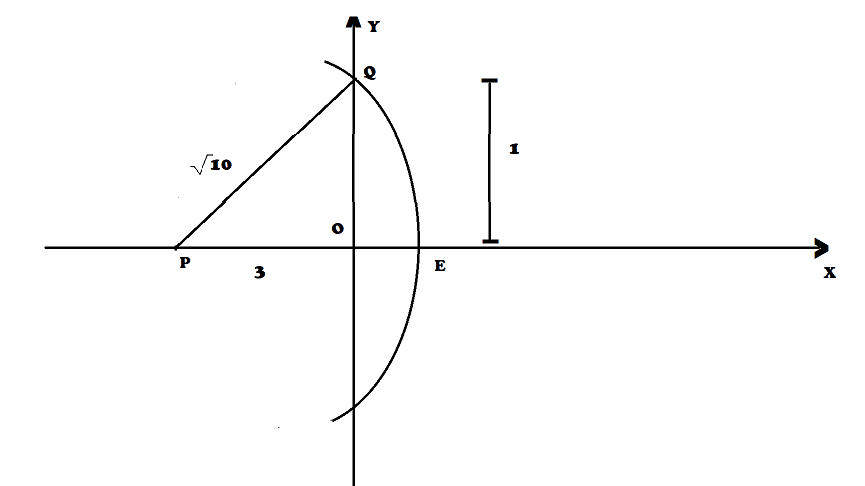
Now, according to this, the steps of construction are as follows :
Step 1. : Take a line segment PO =3 units on the x –axis. (consider 1 unit =2 cm) .
Step 2: Draw a perpendicular on O and draw a line OQ = 1 unit.
Step 3: Now join PQ with
Step 4: Take P as centre and PQ as radius, draw an arc which cuts the x- axis at point E.
Step 5: Now the line segment PQ in the figure represents
Hence, through these steps we had located
Note: In this type of question we should remember some basic points like we should know Pythagoras theorem and basic knowledge of number line and then by using the Pythagoras theorem we will find out the things like hypotenuse, perpendicular and base. Hence by doing step by step construction, we will locate the given number on the number line.
Complete step-by-step solution:
Here , we have to locate
We will do this by using the Pythagoras theorem.
Here, we can write
We know that , according to Pythagoras theorem ,
By comparing this with equation (i) ,we get
Hypotenuse =
Now, according to this, the steps of construction are as follows :
Step 1. : Take a line segment PO =3 units on the x –axis. (consider 1 unit =2 cm) .
Step 2: Draw a perpendicular on O and draw a line OQ = 1 unit.
Step 3: Now join PQ with
Step 4: Take P as centre and PQ as radius, draw an arc which cuts the x- axis at point E.
Step 5: Now the line segment PQ in the figure represents
Hence, through these steps we had located

Note: In this type of question we should remember some basic points like we should know Pythagoras theorem and basic knowledge of number line and then by using the Pythagoras theorem we will find out the things like hypotenuse, perpendicular and base. Hence by doing step by step construction, we will locate the given number on the number line.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What was the capital of the king Kharavela of Kalinga class 9 social science CBSE




