Question

What is the mathematical formula for the area of an irregular trapezoid?

Answer 1

Hint: In this problem we need to calculate the formula for the area of the irregular trapezoid. For this we will first look into what is a trapezoid and derive the formula to calculate the area of the trapezoid. After that we will move to what is an irregular trapezoid and derive the formula for the area of the irregular trapezoid which is our required answer.

Complete step-by-step solution:
We know that the trapezoid is a quadrilateral of having two parallel opposite sides. The diagram of the trapezium is given by

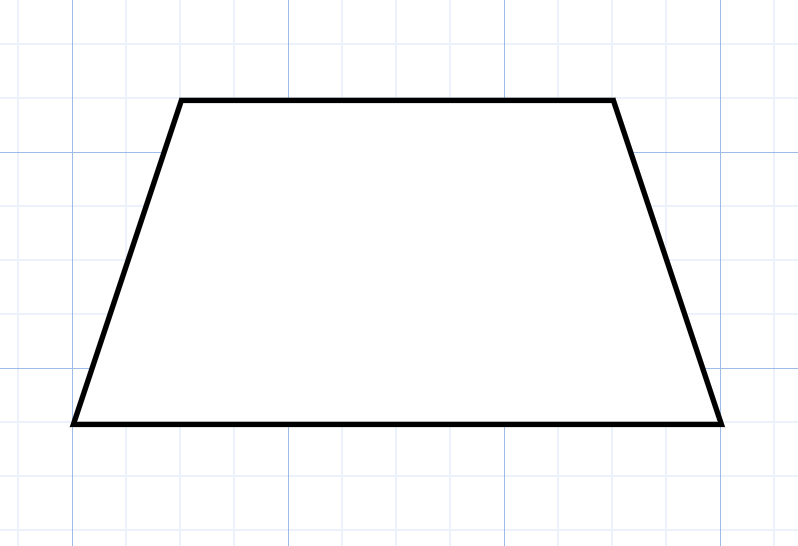
For calculating the area of trapezoid, we are going to assume the following data and reconstruct the diagram as

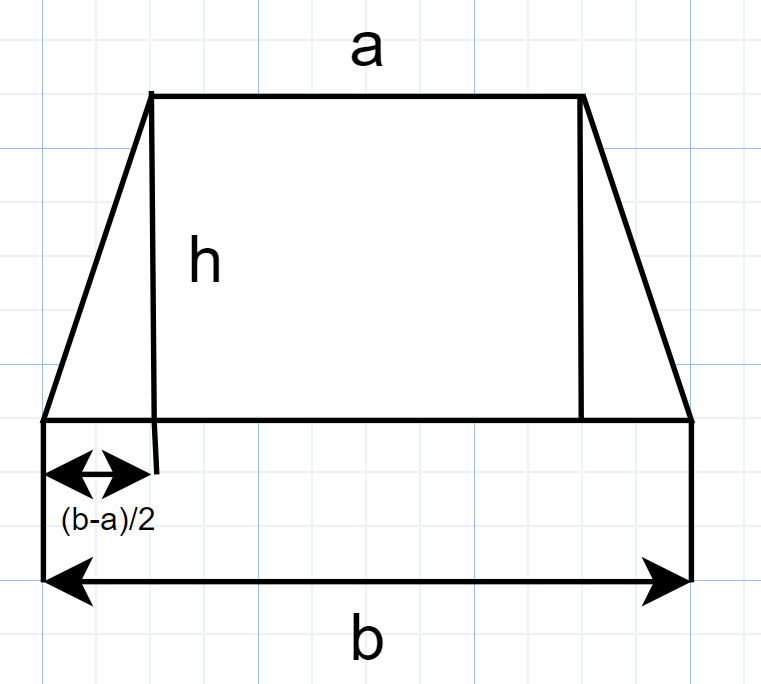
Now we can write the area of the trapezium as sum of $2$ triangles and sum of the rectangle, then we will get
$A=2\left( \dfrac{1}{2}\times \left( \dfrac{b-a}{2} \right)\times h \right)+ah$
Simplifying the above equation, then we will have
$\begin{align}
  & A=\left( \dfrac{b-a}{2} \right)h+ah \\
 & \Rightarrow A=\dfrac{bh}{2}-\dfrac{ah}{2}+ah \\
 & \Rightarrow A=\dfrac{bh}{2}+\dfrac{ah}{2} \\
 & \Rightarrow A=\left( \dfrac{a+b}{2} \right)h \\
\end{align}$
Where $a$, $b$ are the lengths of two parallel sides and $h$ is the perpendicular distance between the two parallel sides.
The above derived formula is used to calculate the area of regular trapezoid that means the length of sloped sides are equal. Irregular trapezoid means the lengths of sloped sides are not the same. The diagram of the irregular trapezoid is given by

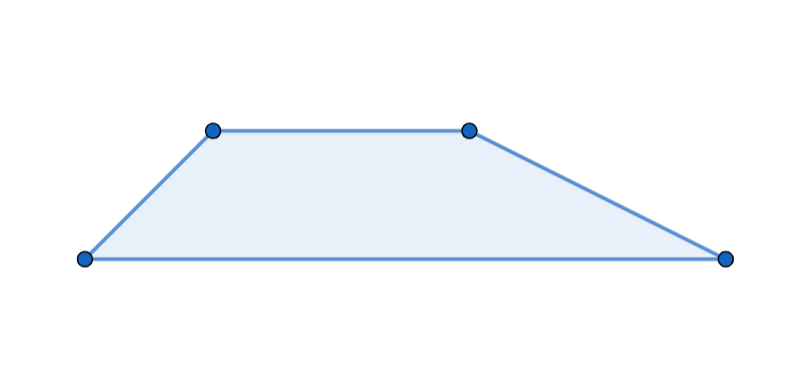
In the above diagram we can observe that the length of side slopes is not the same. So, in order to find the height or perpendicular distance between the two parallel sides we need to have at least one sloped side length and the angle at the sloped side. Now we will use the basic definitions of the trigonometric ratios and calculate the distance between the parallel sides.
After getting the distance between the parallel sides we can use below formula to calculate the area $A=\left( \dfrac{a+b}{2} \right)h$

Note: For the irregular trapezoid we can find the area as the sum of the area of the rectangle and the two triangles that are formed. But here we need to calculate the base as well as height of the two different triangles by using definitions of the trigonometric ratios which will take too much time. So, we can simplify using the above-mentioned method to find the area of the irregular trapezoid.