Question

What do you mean by a linear pair of angles?

Answer 1

Hint: We will first understand the arm and vertex arms and vertex of an angle. Then, we will understand the conditions of linear pairs of angles and put them together to form it.
Complete step-by-step answer:
Angle is a geometric figure which has two rays known as arms of angle meeting at the same endpoint known as vertex of an angle.
Now, a linear pair of angles are two angles which are placed together with four conditions.
First condition is that both the angles should have a common vertex. That is, there will be only one vertex for both the angles.
Second condition is that they should have a common arm. This means that one of the arms of both the angles should be shared by both the angles. That is, they should together have three arms.
Third condition is that the interior part of angles should not overlap. That is, one angle should not cross the other. Therefore, both the angles should be on the opposite side of the common arm.
Fourth condition is that the sum of both the angles should be ${{180}^{\circ }}$. Since, one arm of both the angles is common, they will have no gap between them. Hence, while forming the sum of ${{180}^{\circ }}$, the remaining arms will form a straight line.
Hence the linear pair of angles can be drawn as:
 

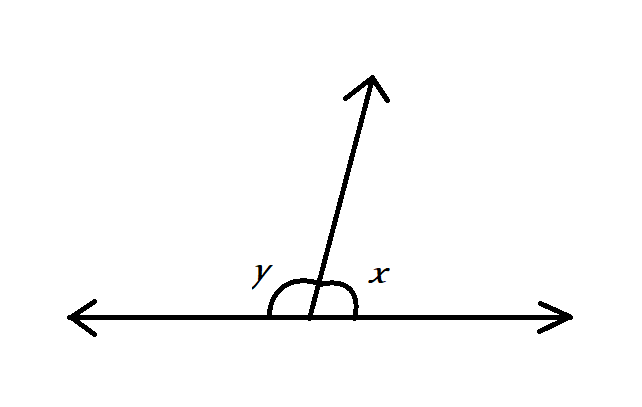
Here angle $x$ and angle $y$ are a pair of linear angles.

Note: Alternative way to understand that, when two straight lines interest, then the pair of angles between them on the upper side or lower side of one of the lines is a linear pair of angels.