Question

What is the measure of one angle of a regular 12 – sided polygon?

Answer 1

Hint: To find the measure of one angle of a regular 12 – sided polygon, first of all we will find the central angle which is constructed by joining two consecutive vertices of the polygon with the centre. We will find this angle by dividing ${{360}^{\circ }}$ to 12. Now, using this internal angle, we can find the internal angle of the 12 – sided polygon.

Complete step by step answer:
We have given a regular 12 – sided polygon which we have constructed in the below:

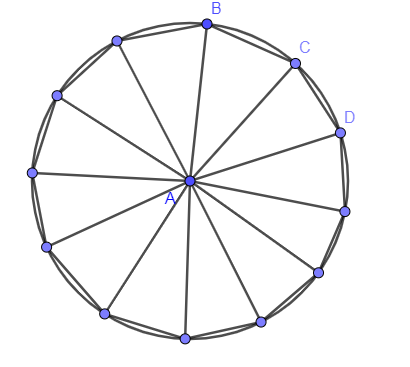
Now, we are going to find the internal angle which is formed by joining the two consecutive vertices with the centre which we can see in the above figure, $\angle BAC$ is the internal angle made by the two consecutive vertices B and C. This internal angle is calculated by dividing ${{360}^{\circ }}$ by 12 as follows:
$\dfrac{{{360}^{\circ }}}{12}$
The numerator and the denominator of the above fraction will get divided by 12 and we get,
$\dfrac{{{30}^{\circ }}}{1}={{30}^{\circ }}$
Now, in $\Delta BAC$, we know the angle $\angle BAC$ and the two sides BA and CA are equal so the angles opposite to it are also equal.
$\angle ABC=\angle BCA$
Let us assume the above two angles as x and we are showing this angle in the above figure and we get,

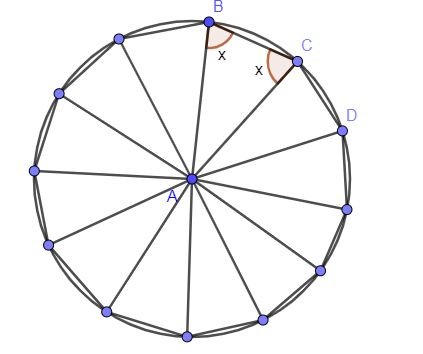
Now, we know that sum of all the angles of a triangle is ${{180}^{\circ }}$ so adding all the three angles of a $\Delta BAC$ and equating it to ${{180}^{\circ }}$.
$\begin{align}
  & x+x+{{30}^{\circ }}={{180}^{\circ }} \\
 & \Rightarrow 2x+{{30}^{\circ }}={{180}^{\circ }} \\
\end{align}$
Subtracting ${{30}^{\circ }}$ on both the sides of the above equation we get,
$\begin{align}
  & 2x={{180}^{\circ }}-{{30}^{\circ }} \\
 & \Rightarrow 2x={{150}^{\circ }} \\
\end{align}$
Now, as the given polygon is a regular polygon so all the neighboring angles are also equal so the above figure will look as:

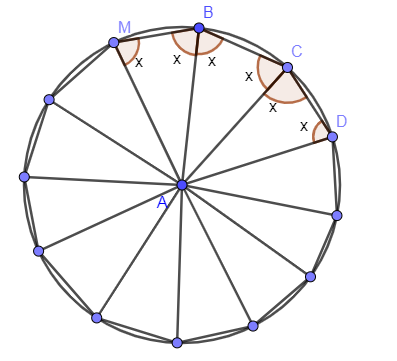
From the figure, you can see that $\angle CBA=\angle MBA=x$ so the one of the angle of the polygon $\angle B$ is equal to the addition of x with x which will give us $2x$ so the angle of the polygon which has been asked in the above question is $2x$ and we have shown above that value of $2x={{150}^{\circ }}$.
Hence, the measure of one angle of a regular 12 – sided polygon is equal to ${{150}^{\circ }}$.

Note: The point to be noted is that this is the regular polygon so all the 12 sides and the 12 angles are equal to this polygon. From this problem, we have learnt that the measure of any one angle of a regular 12 – sided polygon is ${{150}^{\circ }}$. Apart from the derivation of how we come to this angle, you can also remember the value of this angle.