Question

Natural frequency of a simple pendulum depends on-
(A). it’s mass
(B). its length
(C). square of its length
(D). square root of inverse of its length

Answer 1

Hint: The motion of a simple pendulum is a periodic motion about its mean position. Its natural frequency is provided by the component of gravitational force acting on it. This means that in the absence of friction, it will continue to oscillate with its natural frequency. Applying Newton’s second law, we can find an equation for the motion of a simple pendulum.
Formulas Used:
\[\tau =I\alpha \]
\[\tau =Fr\]

Complete answer:
A simple pendulum is a system in which a point mass is suspended from a rod of negligible mass or a string. When displaced from its mean position, it swings and displaces about a mean position and follows a periodic motion. Applying Newton’s second law to the rotational motion of simple pendulum, we get,
\[\tau =I\alpha \] - (1)
Here,
\[\tau \]is the torque acting on the pendulum
\[I\]is the moment of inertia
\[\alpha \]is angular acceleration
Also,
\[\tau =Fr\] - (2)
Here, \[F\]is the force acting on the body
\[r\]is distance from axis of rotation
 

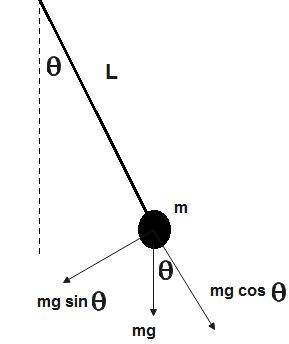
Also torque is provided by the component of mg-\[mg\,\cos \theta \]
 Therefore, from eq (1) and eq (2), we get,
\[m{{L}^{2}}\dfrac{{{d}^{2}}\theta }{d{{t}^{2}}}=-(mg\,\sin \theta )L\] [\[I=m{{L}^{2}}\] and \[\alpha =\dfrac{{{d}^{2}}\theta }{d{{t}^{2}}}\] ]
Rearranging the above equation as-
\[\dfrac{{{d}^{2}}\theta }{d{{t}^{2}}}+\dfrac{g\,\sin \theta }{L}=0\]
If \[\begin{align}
  & \theta <<1 \\
 & \Rightarrow \,\sin \theta \approx \theta \\
\end{align}\]
Therefore, the above equation will be-
\[\dfrac{{{d}^{2}}\theta }{d{{t}^{2}}}+\dfrac{g\,\theta }{L}=0\] [Equation for simple harmonic motion]
the above equation reduces to the equation of simple harmonic motion
 In simple harmonic motion, change in phase takes place as-
\[\theta (t)={{\theta }_{0}}\cos (\omega t+\phi )\]
Here, \[\theta \] is the angle with which the pendulum gets displaced about its mean position
\[\omega \] is the angular velocity
\[t\]is time taken
The angular velocity in simple harmonic motion is given by-
\[\begin{align}
  & \omega =\sqrt{\dfrac{g}{L}} \\
 & \therefore f=\dfrac{1}{2\pi }\sqrt{\dfrac{g}{L}} \\
\end{align}\]
 \[f=\dfrac{1}{2\pi }\sqrt{\dfrac{g}{L}}\] is the natural frequency of the motion of a simple pendulum
The natural frequency is \[f=\dfrac{1}{2\pi }\sqrt{\dfrac{g}{L}}\] and it depends on square root of inverse of its length.,

So the correct option is (D).

Note:
Harmonic motion is the motion about an equilibrium position such that the maximum displacement on both sides of the mean position is equal. In this type of motion, the restoring force towards the equilibrium position is directly proportional to the negative of maximum displacement.