
Observe the given boundary surface diagrams of two orbitals I and II and choose the correct option.
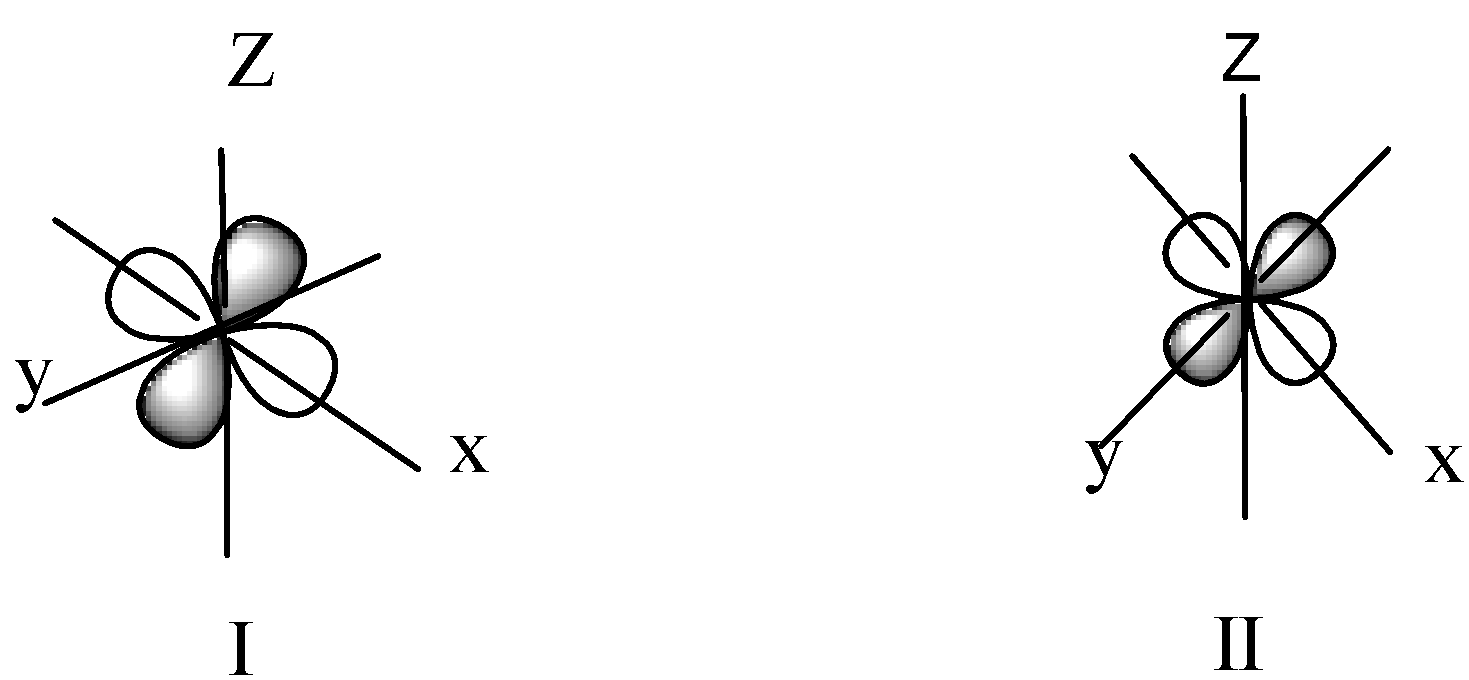
A) $I - {d_{{x^2} - {y^2}}}$,$II - {d_{yz}}$
B) $I - {d_{yz}}$,$II - {d_{{x^2} - {y^2}}}$
C) $I - {d_{xz}}$,$II - {d_{{z^2}}}$
D) $I - {d_{xy}}$,$II - {d_{xz}}$
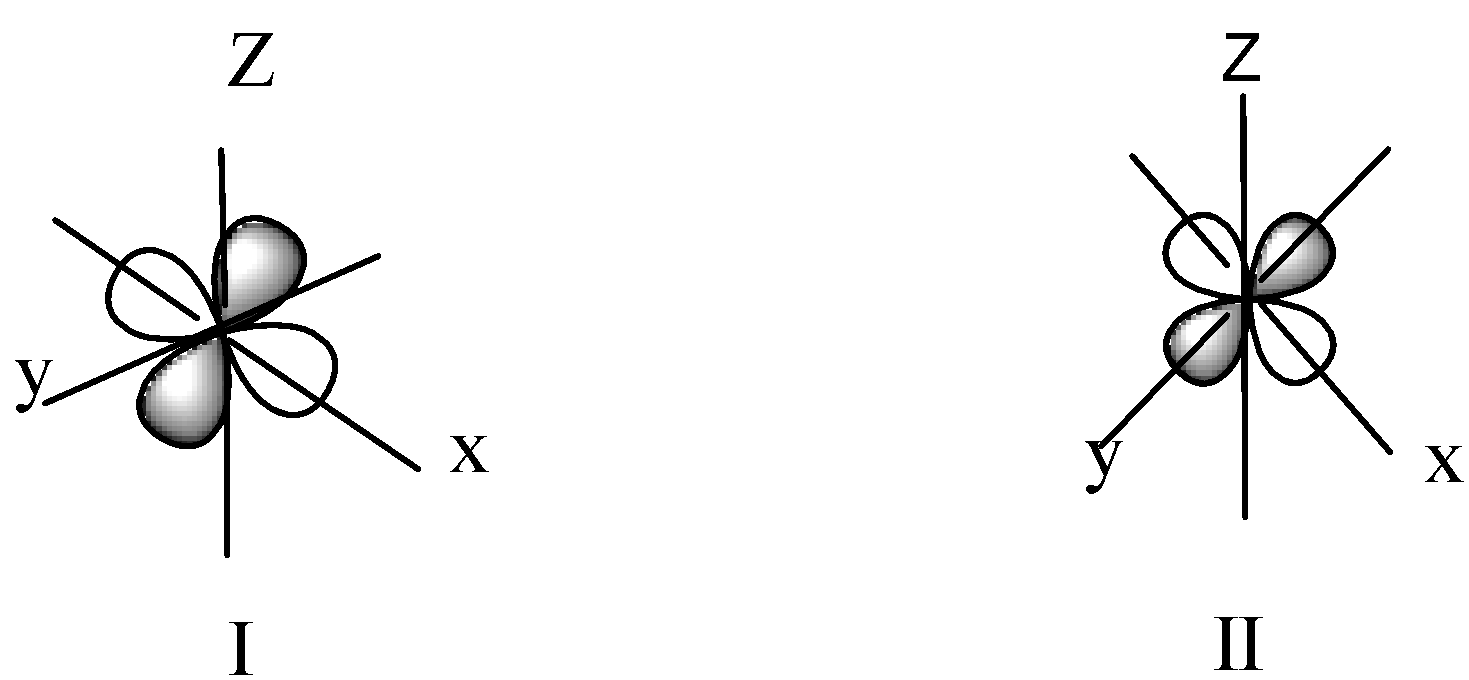
Answer
456k+ views
Hint:We know that boundary surface chart is a decent diagrammatical portrayal of states of nuclear orbitals. It is resultant of the arrangement of Schrödinger wave conditions. As we realize that the specific position and energy of an electron can't be resolved, so we compute the likelihood of finding an electron in a specific area. Limit surface graph is a limit surface or a form surface attracted a space for an orbital on which the estimation of likelihood thickness \[\left| \psi \right|2\] is steady.
Complete step by step answer:
We know that the shape of d- orbitals are Double dumbbell-shaped. In this shape lobes are locate in the d-orbitals. As we know ${d_{{z^2}}}$ -orbital has one lobe along z-axis and the shape of ${d_{{z^2}}}$orbital is donut-shape an electron clouds are perpendicular to it in xy plane. The \[{d_{xy\;}}\] have two dumbbell-shaped lobes among the x-y axis. \[{d_{yz}}\;\] have two dumbbell-shaped lobes among the y-z axis. \[{d_{zx}}\] have two dumbbell-shaped lobes among the z-x axis. \[{d_{{x^2}}}_{ - {y^2}\;}\] has two lobes along the x and y-axis.
The given boundary chart is,
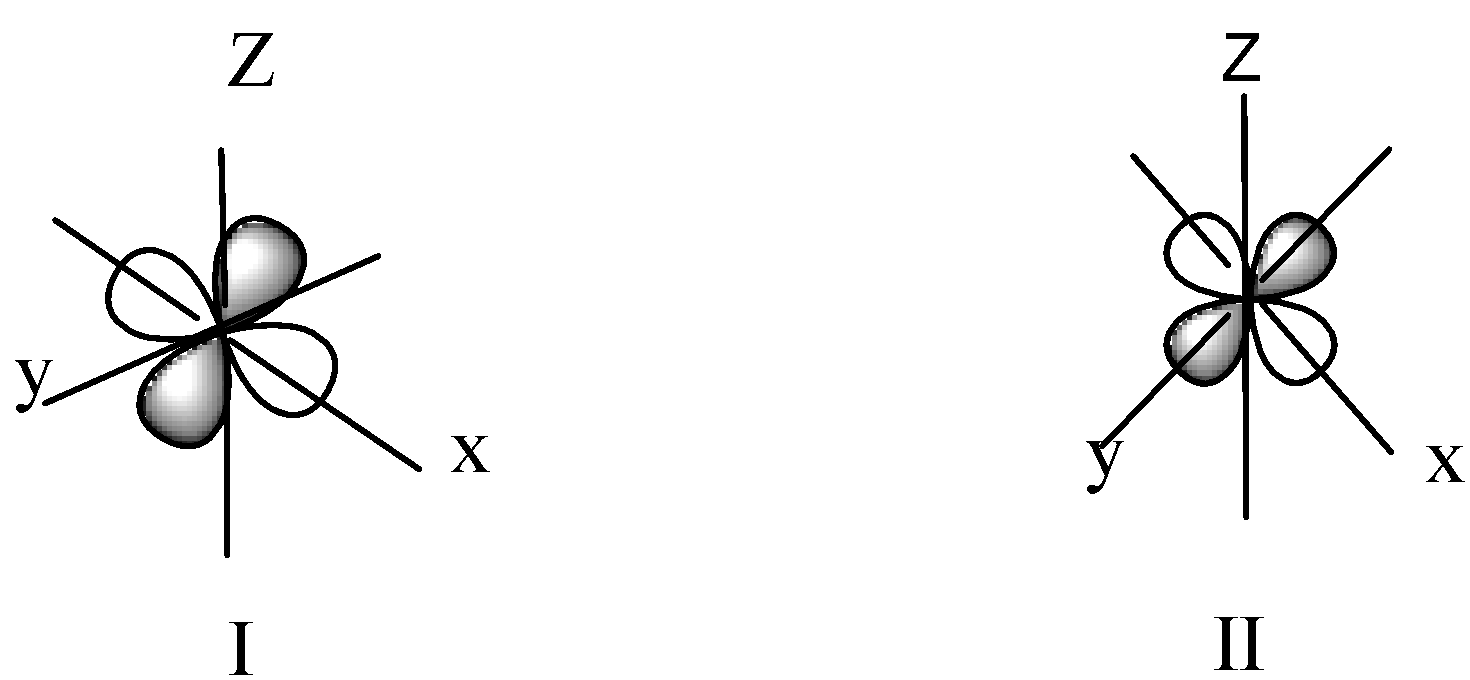
In diagram I, lobes are among the y-z axis and in diagram II the two lobes along the x and y-axis.
Hence option B is correct.
Note:
We can discuss some of the features of boundary charts as below.
-Shape of the surface chart: The boundary surface chart of an orbital is autonomous of guideline quantum number. For e.g.: The boundary surface chart of s orbital is round, so it will be circular for 1s, 2s, 3s and 4s or for any broad ns. The shape doesn't rely upon the principal quantum number.
-Size of the surface chart: The boundary surface outline of an orbital expansion in size or volume with increment on a principal quantum number.
-Nodes in the surface outline: Nodes are the districts with low likelihood thickness commonly which goes to zero. There are \[\left( {n - 1} \right)\] nodes in the limit surface chart of s-orbital with 'n' principal quantum number. This sort of hub is likewise seen in the surface graph of p, d and f orbitals.
Complete step by step answer:
We know that the shape of d- orbitals are Double dumbbell-shaped. In this shape lobes are locate in the d-orbitals. As we know ${d_{{z^2}}}$ -orbital has one lobe along z-axis and the shape of ${d_{{z^2}}}$orbital is donut-shape an electron clouds are perpendicular to it in xy plane. The \[{d_{xy\;}}\] have two dumbbell-shaped lobes among the x-y axis. \[{d_{yz}}\;\] have two dumbbell-shaped lobes among the y-z axis. \[{d_{zx}}\] have two dumbbell-shaped lobes among the z-x axis. \[{d_{{x^2}}}_{ - {y^2}\;}\] has two lobes along the x and y-axis.
The given boundary chart is,
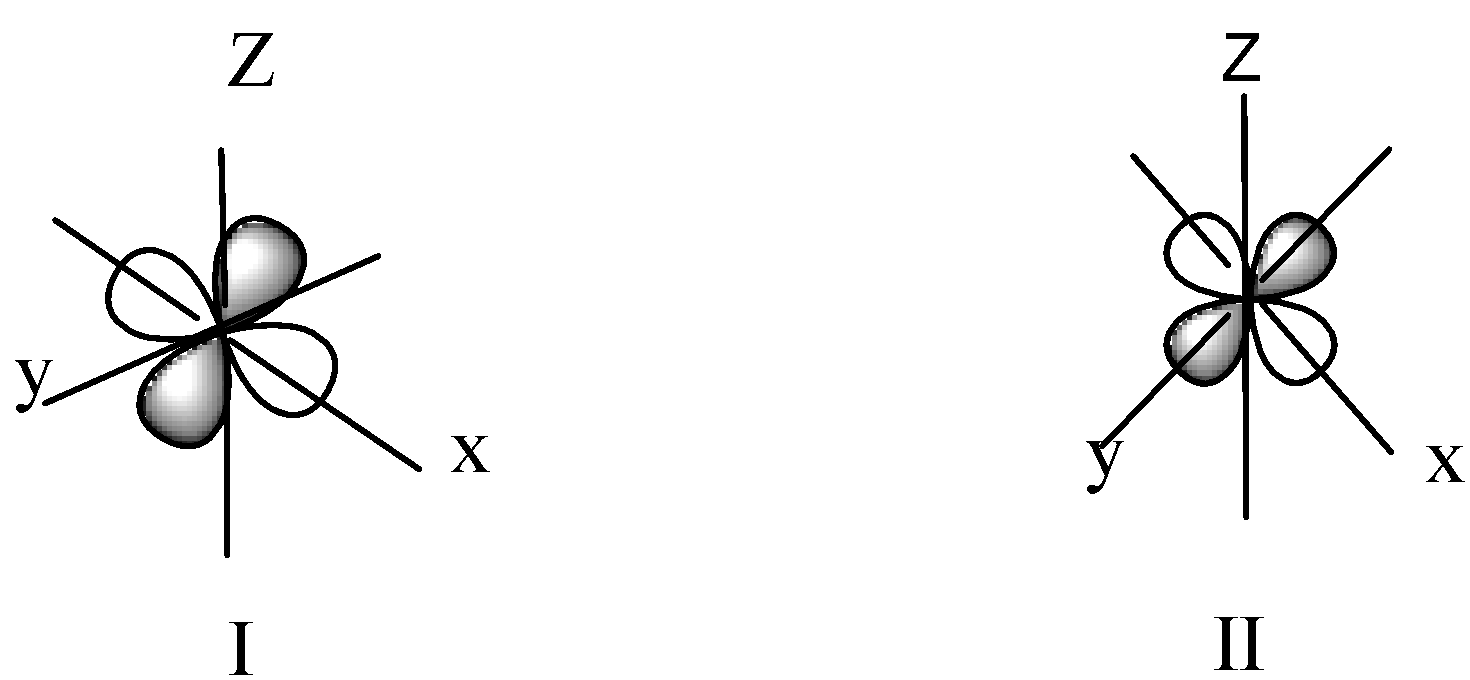
In diagram I, lobes are among the y-z axis and in diagram II the two lobes along the x and y-axis.
Hence option B is correct.
Note:
We can discuss some of the features of boundary charts as below.
-Shape of the surface chart: The boundary surface chart of an orbital is autonomous of guideline quantum number. For e.g.: The boundary surface chart of s orbital is round, so it will be circular for 1s, 2s, 3s and 4s or for any broad ns. The shape doesn't rely upon the principal quantum number.
-Size of the surface chart: The boundary surface outline of an orbital expansion in size or volume with increment on a principal quantum number.
-Nodes in the surface outline: Nodes are the districts with low likelihood thickness commonly which goes to zero. There are \[\left( {n - 1} \right)\] nodes in the limit surface chart of s-orbital with 'n' principal quantum number. This sort of hub is likewise seen in the surface graph of p, d and f orbitals.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

What is a transformer Explain the principle construction class 12 physics CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

What are the major means of transport Explain each class 12 social science CBSE

What is the Full Form of PVC, PET, HDPE, LDPE, PP and PS ?




