Question

What is the opposite of exponential growth?

Answer 1

Hint: We start the problem by recalling the basic definition of exponential function and also, we can recall the definition of exponential growth & exponential decay and also formula of exponential growth We can solve examples of exponential growth and after that we can go to opposite of exponential growth.

Complete step-by-step solution:
Exponential function:
An exponential function can be defined as in the form of \[f\left( x \right)={{a}^{x}}..................(i)\]
,where ‘a’ is known as the base of the function and it should be always greater than zero and ‘x’ is the variable.
The exponential function is generally denoted by ‘e’.
Exponential growth:
The exponential growth quantity increases slowly at first and then it increases quickly. Its rate of change depends on time. As time increases, the rate of growth also increases. The increase in the growth is known as ‘exponential increase’.
the expression for Exponential growth is
\[y={{\left( 1+r \right)}^{x}}................(ii)\], r denotes the growth percentage.
When we compare both equations & ,
\[\Rightarrow \] \[a=\left( 1+r \right)\]
Exponential decay:
The exponential decay quantity decreases very quickly at first, and then it decreases. It is generally decreasing with time. As time decreases, the rate of change becomes slower. Decrease in the rate of change is generally called ‘exponential decrease’.
The expression for exponential growth is denoted by:
\[\Rightarrow \] \[y={{\left( 1-r \right)}^{x}}................(iii)\]
Hence, equation & indicates the increase or decrease of exponential growth.
 Opposite of Exponential growth is the ‘logarithmic growth’ and is very slow.
Logarithmic growth: it is described by a phenomenon whose cost or size could be described as a logarithm function, which is in the form of \[y=C\log x\].
Here, any logarithm base could be used, if one can be converted to another by multiplying with a fixed constant.

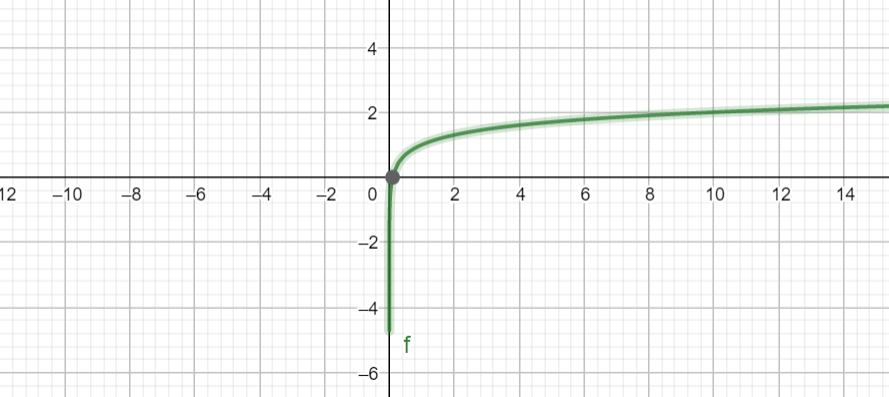
This graph depicts logarithmic growth.

Note: The common mistakes done by the students is mapping the graph according to the points and confusion at the logarithm and exponential forms. Also, one can make mistakes by misunderstanding the opposite of exponential growth as the differential or integral of exponential function. So, we have to be careful.