Question

Out of 100 students 15 passed in English, 12 passed in Mathematics, 8 in Science,6 in English and Mathematics, 7 in Mathematics and Science, 4 in English and Science, 4 in all the three. Find how many passed in English and mathematics but not in science?

Answer 1

Hint: For solving this problem, first draw the Venn diagram of the situation by analyzing the statement provided in the problem. Now we assign different values to different parts of the circle. By using this data representation, we can easily evaluate our answer.
Complete step by step answer:
The Venn diagram for our problem could be represented as:

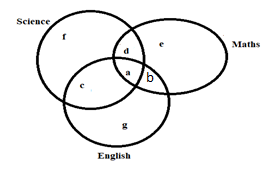
According to the problem statement, total number of students (U) = 100, number of students passed in English = n(E) = 15, number of students passed in Math’s = n(M) = 12 and number of students passed in Science = n(S) = 8.
The intersection of two events is defined as the occurrence of both events at one time. It is represented by $\cap $. Now, other statements could be represented as:
Number of students passed in both English and math =\[n(E\cap M)=6\]
Number of students passed in Math and Science =\[n(S\cap M)=6\]
Number of students passed in English and science$=n(E\cap S)=4$
Number of students passed in all 3 subjects$=n(E\cap M\cap S)=4$
By using the representation from Venn diagram, we get values for different variables such as a, b, c, d, e, f and g as concluded from the above statements. So, their respective values are:
\[\begin{align}
  & a=n(E\cap M\cap S)=4 \\
 & a+d=n(M\cap S)=7 \\
 & d=7-4 \\
 & \therefore d=3 \\
 & a+b=n(M\cap E)=6 \\
 & b=6-4 \\
 & \therefore b=2 \\
 & a+c=n(S\cap E)=4 \\
 & c=4-4 \\
 & \therefore c=0 \\
\end{align}\]
Hence, the number of students passed in English and Mathematics but not in science is displayed by c in the Venn diagram. The obtained value of c = 0.
Therefore, the number of students passed in English and Mathematics but not in science is 0.

Note: The key concept involved in solving this problem is the knowledge of Venn diagrams. Students must not get confused by seeing the area of c in the Venn diagram. The above representation is a possible representation but the value on calculation is the correct value.