Question

Out of $\text{ }{{\text{C}}_{2}}\text{ }$, $\text{ }{{\text{F}}_{2}}\text{ }$, $\text{ }{{\text{O}}_{2}}\text{ }$, $\text{ NO }$which will be stabilized after forming anion?
A) $\text{ }{{\text{C}}_{2}}\text{ }$
B) $\text{ }{{\text{F}}_{2}}\text{ }$
C) $\text{ }{{\text{O}}_{2}}\text{ }$
D) $\text{ NO }$

Answer 1

Hint: The stability of a molecule can be explained based on the molecular orbital theory. The MOT comprises bonding and antibonding orbitals. When the extra electrons from the negative charge enters into the bonding orbitals stabilizes the molecules, however, if the last electrons enter into the antibonding orbital then it contributes towards the stability of the molecule. Thus, one can say the bond order is directly related to the bond order. The relation is,
$\text{ Bond order }\propto \text{ Stability }$.
Based on the MOT diagram we can determine which anion will be stable.

Complete step by step answer:
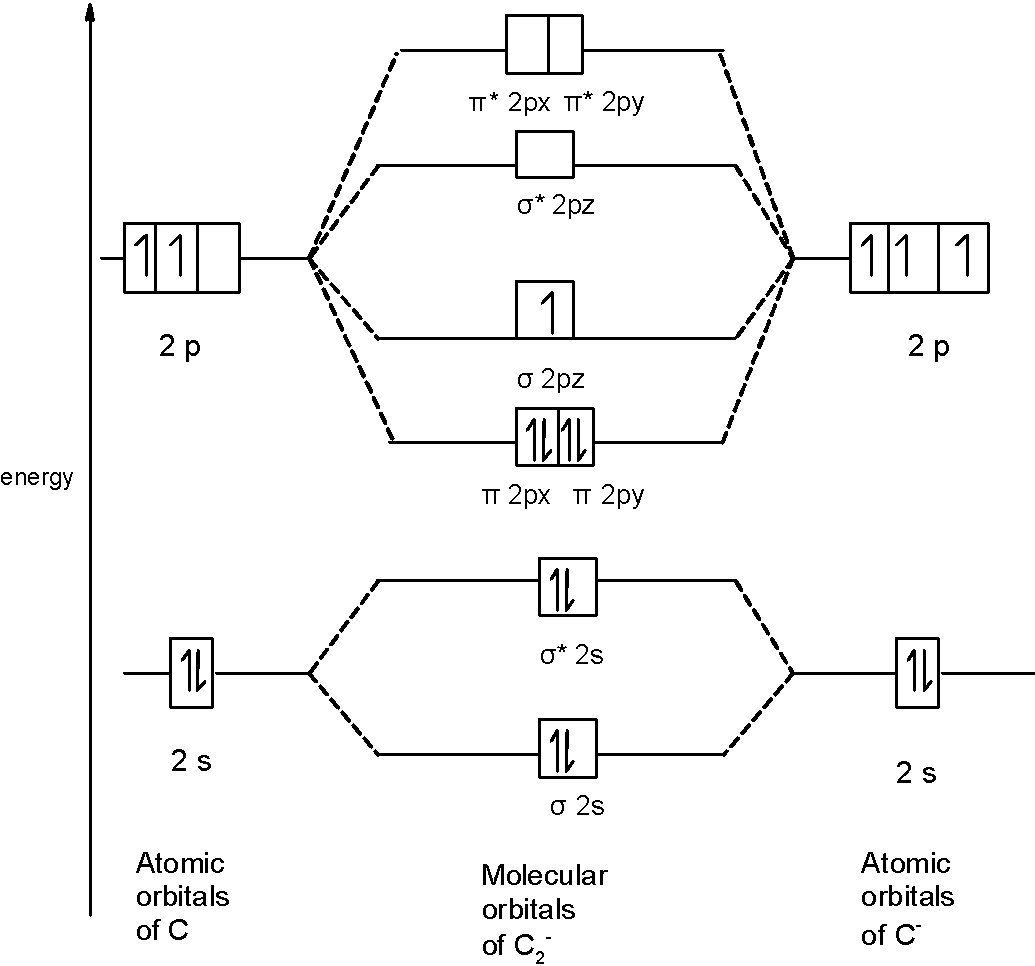
A) $\text{ }{{\text{C}}_{2}}^{-}\text{ }$ molecule:
First of all, we can write the molecular orbital configuration of$\text{ }{{\text{C}}_{2}}^{-}\text{ }$ the molecule. In an $\text{ }{{\text{C}}_{2}}^{-}\text{ }$anion molecule, there are a total of 13 electrons. The molecular orbital configuration of $\text{ }{{\text{C}}_{2}}^{-}\text{ }$the molecule is as follows:
\[\]$\text{ }\!\!\sigma\!\!\text{ 1}{{\text{s}}^{\text{2}}}\text{,}{{\text{ }\!\!\sigma\!\!\text{ }}^{\text{*}}}\text{1}{{\text{s}}^{\text{2}}}\text{, }\!\!\sigma\!\!\text{ 2}{{\text{s}}^{\text{2}}}\text{, }{{\text{ }\!\!\sigma\!\!\text{ }}^{\text{*}}}\text{2}{{\text{s}}^{\text{2}}}\text{, 2p}_{\text{x}}^{\text{2}}\text{ }\!\!\pi\!\!\text{ = 2p}_{\text{y}}^{\text{2}}\text{ }\!\!\pi\!\!\text{ , }\!\!\sigma\!\!\text{ 2}{{\text{p}}^{1}}_{z}$. There are 9 bonding and 4 nonbonding electrons in the orbitals according to the molecular orbital configuration. Therefore, $\text{ Bond order =}\dfrac{\text{1}}{\text{2}}\left[ \text{Bonding-antibonding} \right]=\dfrac{1}{2}\left[ 9-4 \right]=\dfrac{1}{2}\left( 5 \right)=2.5$
Thus, the bond order $\text{ }{{\text{C}}_{2}}^{-}\text{ }$ is 2.5.

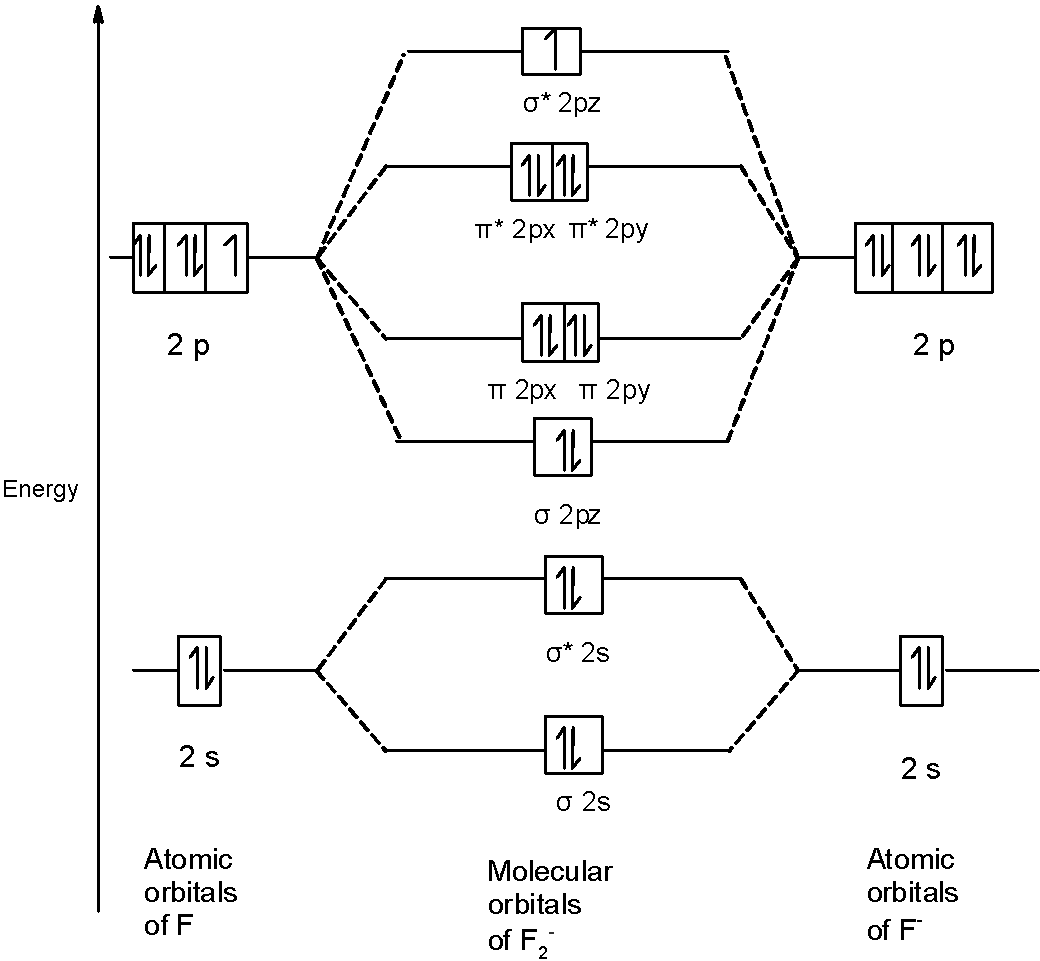
B) $\text{ }{{\text{F}}_{2}}^{-}\text{ }$ Molecule: We can write the molecular orbital configuration of $\text{ }{{\text{F}}_{2}}^{-}\text{ }$ the molecule. In an $\text{ }{{\text{F}}_{2}}^{-}\text{ }$anion molecule, there are a total of 13 electrons. The molecular orbital configuration of $\text{ }{{\text{F}}_{2}}^{-}\text{ }$ the molecule is as follows:
\[\]$\text{ }\!\!\sigma\!\!\text{ 1}{{\text{s}}^{\text{2}}}\text{,}{{\text{ }\!\!\sigma\!\!\text{ }}^{\text{*}}}\text{1}{{\text{s}}^{\text{2}}}\text{, }\!\!\sigma\!\!\text{ 2}{{\text{s}}^{\text{2}}}\text{, }{{\text{ }\!\!\sigma\!\!\text{ }}^{\text{*}}}\text{2}{{\text{s}}^{\text{2}}}\text{, }\!\!\sigma\!\!\text{ 2}{{\text{p}}^{2}}_{z},\text{2p}_{\text{x}}^{\text{2}}\text{ }\!\!\pi\!\!\text{ = 2p}_{\text{y}}^{2}\text{ }\!\!\pi\!\!\text{ , 2p}_{\text{x}}^{\text{2}}\text{ }\!\!\pi\!\!\text{ * = 2p}_{\text{y}}^{2}\text{ }\!\!\pi\!\!\text{ *, }\!\!\sigma\!\!\text{ *2}{{\text{p}}^{1}}_{z}$ There are 10 bonding and 9 nonbonding electrons in the orbitals according to the molecular orbital configuration. Therefore, $\text{ Bond order =}\dfrac{\text{1}}{\text{2}}\left[ \text{Bonding-antibonding} \right]=\dfrac{1}{2}\left[ 10-9 \right]=\dfrac{1}{2}\left( 1 \right)=0.5$ Thus, the bond order $\text{ }{{\text{F}}_{2}}^{-}\text{ }$ is 0.5.

C) $O_{2}^{-}$ Molecule: In $O_{2}^{-}$ a molecule, there are 17 electrons. The MOT diagram holds a total of 17 electrons. The MOT diagram is as shown below,

So, the molecular orbital configuration is as follows:
$\text{ }\!\!\sigma\!\!\text{ 1}{{\text{s}}^{\text{2}}}\text{,}{{\text{ }\!\!\sigma\!\!\text{ }}^{\text{*}}}\text{1}{{\text{s}}^{\text{2}}}\text{, }\!\!\sigma\!\!\text{ 2}{{\text{s}}^{\text{2}}}\text{, }{{\text{ }\!\!\sigma\!\!\text{ }}^{\text{*}}}\text{2}{{\text{s}}^{\text{2}}}\text{, }\!\!\sigma\!\!\text{ 2}{{\text{p}}^{\text{2}}}_{z}\text{, 2p}_{\text{x}}^{\text{2}}\text{ }\!\!\pi\!\!\text{ = 2p}_{\text{y}}^{\text{2}}\text{ }\!\!\pi\!\!\text{ , 2p}_{\text{x}}^{\text{2}}{{\text{ }\!\!\pi\!\!\text{ }}^{\text{*}}}\text{=2p}_{\text{y}}^{1}{{\text{ }\!\!\pi\!\!\text{ }}^{\text{*}}}$ There are 10 bonding electrons (including molecular orbitals formed by the $\text{1s}$ orbitals.) and 7 nonbonding electrons. $\text{ Bond order =}\dfrac{\text{1}}{\text{2}}\left[ \text{Bonding-antibonding} \right]=\text{ }=\dfrac{1}{2}\left[ 10-7 \right]=1.5$. Therefore, the bond order $O_{2}^{-}$ is$1.5$.

D) $\text{ N}{{\text{O}}^{-}}$ Molecule: In $\text{ N}{{\text{O}}^{-}}$ a molecule, there are 16 electrons. The MOT diagram holds a total of 17 electrons. The MOT diagram is as shown below,

So, the molecular orbital configuration is as follows:
$\text{ }\!\!\sigma\!\!\text{ 1}{{\text{s}}^{\text{2}}}\text{,}{{\text{ }\!\!\sigma\!\!\text{ }}^{\text{*}}}\text{1}{{\text{s}}^{\text{2}}}\text{, }\!\!\sigma\!\!\text{ 2}{{\text{s}}^{\text{2}}}\text{, }{{\text{ }\!\!\sigma\!\!\text{ }}^{\text{*}}}\text{2}{{\text{s}}^{\text{2}}}\text{, }\!\!\sigma\!\!\text{ 2}{{\text{p}}^{\text{2}}}_{z}\text{, 2p}_{\text{x}}^{\text{2}}\text{ }\!\!\pi\!\!\text{ = 2p}_{\text{y}}^{\text{2}}\text{ }\!\!\pi\!\!\text{ , 2p}_{\text{x}}^{1}{{\text{ }\!\!\pi\!\!\text{ }}^{\text{*}}}\text{=2p}_{\text{y}}^{1}{{\text{ }\!\!\pi\!\!\text{ }}^{\text{*}}}$
There are 10 bonding electrons (including molecular orbitals formed by the $\text{1s}$ orbitals.) and 6 nonbonding electrons. Therefore, $\text{ Bond order =}\dfrac{\text{1}}{\text{2}}\left[ \text{Bonding-antibonding} \right]=\text{ }=\dfrac{1}{2}\left[ 10-6 \right]=2.0$. Therefore, the bond order$\text{ N}{{\text{O}}^{-}}$ is 2. The bond order is directly related to the bond order. The relation is, $\text{ Bond order }\propto \text{ Stability }$.Thus form the bond order the order of stability is as shown below, $\text{ }{{\text{C}}_{2}}^{-}\text{ }>\text{ N}{{\text{O}}^{-}}\text{ }>O_{2}^{-}\text{ }>\text{ F}_{2}^{-}\text{ }$

Hence, (A) is the correct option.

Note: The MOT diagram for the heteronuclear molecules is drawn in such a manner that the atom which has high electronegativity is written lower in energy than one which has the less electronegative character. Therefore, in the diagram, the atomic orbitals of oxygen are lower as compared to the atomic orbitals of nitrogen. However, there is no electronegativity difference in diatomic molecules thus AO is placed on the same energy level.