Question

What is the packing efficiency for an end centered unit cell?

Answer 1

Hint- The packing efficiency can be calculated by the percent of space occupied by spheres present in a unit cell. Here we will proceed further by evaluating the volume of spheres in the unit cell and total volume of the unit cell.

Complete answer:
We will use the following figure of the end centered unit cell to solve the problem.

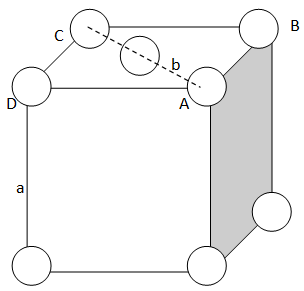
Let the side of an unit cell = a
And diagonal AC = b
Now, in right triangle ABC,
Let us use the Pythagoras theorem.
AD is perpendicular, DC is base and AC is diagonal
$
  \because A{C^2} = A{D^2} + D{C^2} \\
   \Rightarrow {b^2} = {a^2} + {a^2} \\
   \Rightarrow {b^2} = 2{a^2} \\
   \Rightarrow b = \sqrt 2 a \\
 $
Let r is the radius of sphere, so b = 4r,
Thus,
\[
  b = 4r = a\sqrt 2 \\
   \Rightarrow a = \dfrac{{4r}}{{\sqrt 2 }} \\
   \Rightarrow a = \dfrac{{4r}}{{\sqrt 2 }} \times \dfrac{{\sqrt 2 }}{{\sqrt 2 }} \\
   \Rightarrow a = \dfrac{{4\sqrt 2 r}}{2} \\
   \Rightarrow a = 2\sqrt 2 r.........(1) \\
 \]
Now, volume of cube $ = {\left( {{\text{side}}} \right)^3} = {a^3}$
Substituting the value of a from equation (i) we get,
Volume of cube
$
   = {a^3} = {\left( {2\sqrt 2 r} \right)^3} \\
   = 8 \times 2\sqrt 2 \times {r^3} \\
   = 16\sqrt 2 {r^3} \\
 $
Volume of cube $ = 16\sqrt 2 {r^3}$ ---- (2)
Now, volume of sphere
$ = \dfrac{4}{3}\pi {r^3}..........(3)$
Since one unit cell of end entered cell has 2 spheres
$ = \dfrac{1}{8} \times 8 + \dfrac{1}{2} \times 2 = 1 + 1 = 2$
As the contribution of the corner sphere in a cell is one eighth and that of the face sphere is half.
Therefore, volume of 2 atoms, i.e. 2 spheres:
$
   = 2 \times \dfrac{4}{3}\pi {r^3} \\
   = \dfrac{8}{3}\pi {r^3} \\
 $
We know that

 Packing efficiency = (Volume of spheres in unit cell/ total volume of unit cell) × 100%
Since there are 2 atoms in the unit cell of end centered cell
Therefore, packing efficiency of end centered cell
Packing efficiency = (Volume of 2 spheres in unit cell/ total volume of unit cell) × 100%
Now, packing efficiency (in %)
$
   = \dfrac{{{\text{volume of 2 spheres in unit cell}}}}{{{\text{total volume of unit cell}}}} \times 100 \\
   = \dfrac{{\dfrac{8}{3}\pi {r^3}}}{{16\sqrt 2 {r^3}}} \times 100 \\
 $
Let us solve the equation by cancelling the common term to find the percentage.
$
   = \dfrac{{8\pi }}{{3 \times 16\sqrt 2 }} \times 100 \\
   = \dfrac{{\pi \times 100}}{{3 \times 2\sqrt 2 }} \\
   = \dfrac{{3.14 \times 50}}{{3 \times 1.414}} \\
   = 37.02\% \\
 $

Hence, packing efficiency for end centered unit cell is 37.02%

Note- Packing efficiency is defined as the percentage of space occupied by constituent particles packed inside the lattice. It can be calculated with the help of geometry in three structures namely: HCP and CCP structures. The packing efficiency of simple cubic lattice is 52.4%. And the packing efficiency of body centered cubic lattice (bcc) is 68%.